Espace projectif
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 13:55
par barbu23 » 06 Oct 2012, 13:55
Bonjour;
Il y'a un passage dans mon cours que je ne comprends pas bien :
On dit que
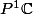
est une variété différentielle lisse de dimension

, dont un atlas est
 , ( U_1 , \varphi_1 ) \} $)
, où :
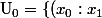 \in P^1 \mathbb{C} \ , \ x_0 \neq 0 \} \ $)
et
 & \longrightarrow & \frac{x_{1}}{x_{0}} \end{cases} $)
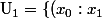 \in P^1 \mathbb{C} \ , \ x_1 \neq 0 \} \ $)
et
 & \to & \frac{x_{0}}{x_{1}} \end{cases} $) Questions :
Questions :- Pourquoi
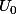
et
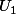
sont des ouverts de
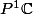
?
- Pourquoi
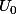
et
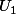
recouvrent
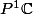
?
- Pourquoi

et

sont des homéomorphismes ?
Merci d'avance.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 14:46
par barbu23 » 06 Oct 2012, 14:46
Help please. :happy3:
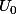
et
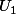
sont des ouverts de
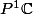
, car
 = \Big( \mathbb{R} \backslash \{ 0 \} \Big) \times \mathbb{R} $)
et
 = \mathbb{R} \times \Big( \mathbb{R} \backslash \{ 0 \} \Big) $)
sont des ouverts de
 \} $)
, non ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 15:11
par Doraki » 06 Oct 2012, 15:11
non.
C'est quoi ta définition de P1C ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 15:21
par barbu23 » 06 Oct 2012, 15:21
Doraki a écrit:non.
C'est quoi ta définition de P1C ?
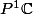
est l'ensemble des droites vectorielles de
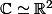
via la relation d'équivalence :
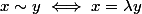
et
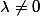
. Est ce que les éléments de
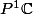
sont uniquement les droites passant par
 $)
? parce que j'ai entendu parler de ça quelque part. Il y'a bijection entre
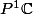
est le cercle
 $)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 15:26
par Doraki » 06 Oct 2012, 15:26
Non P1C est l'ensemble des droites vectorielles du C-espace vectoriel C².
P1R est l'ensemble des droites vectorielles du R-espace vectoriel R², qui n'a absolument aucune raison de devoir être identifié à C (ça n'apporte absolument rien).
Une droite vectorielle ça veut dire un sous-C-espace vectoriel de C² de dimension 1, donc un ensemble de la forme {;)z, ;) dans C} où z est dans C²-{(0,0)}.
Quelle est la topologie sur P1C ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 15:45
par barbu23 » 06 Oct 2012, 15:45
Doraki a écrit:Non P1C est l'ensemble des droites vectorielles du C-espace vectoriel C².
P1R est l'ensemble des droites vectorielles du R-espace vectoriel R², qui n'a absolument aucune raison de devoir être identifié à C (ça n'apporte absolument rien).
Une droite vectorielle ça veut dire un sous-C-espace vectoriel de C² de dimension 1, donc un ensemble de la forme {;)z,

dans C} où z est dans C²-{(0,0)}.
Quelle est la topologie sur P1C ?
C'est la topologie quotient qui rend continue
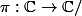
( topologie finale ). :hein:
Moi,
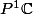
est l'ensemble des droites de
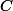
,sinon

et

seront définie autrement non ? on n'aurait pas parlé de
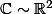
comme ensemble d'arrivée de

, non ? :mur:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 16:03
par Doraki » 06 Oct 2012, 16:03
Bon manifestement tu veux parler de P1R alors. Efface C partout et remplace-le par R², un R-espace vectoriel de dimension 2.
Tu as l'air de penser que l'ensemble des droites vectorielles de R², et R²/~, c'est la même chose.
(où pour tout x et y de R², x~y <=> il existe ;) réel non nul tel que ;).x = ;).y)
Donc j'ai quelques questions.
La droite vectorielle {(x,y) / 2x+3y = 0} ça correspond à quelle classe d'équivalence dans R²/~ ?
La classe d'équivalence de (0,0) (à savoir {(0,0)}) correspond à quelle droite vectorielle de R² ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 16:27
par barbu23 » 06 Oct 2012, 16:27
Je ne peux pas effacer
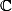
, parce que c'est écrit dans mon cours, je ne peux pas sortir de ce que dit le cours. D'accord, donc
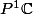
est l'espace
 $)
Pour répondre à tes questions :
-
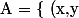 \in \mathbb{R} \ / \ 2x + 3y = 0 \} $)
, donc
 = \{ [x,y] = ( \lambda x , \lambda y ) \in \mathbb{R}^2 / \sim \ / \ 2( \lambda x ) + 3( \lambda y) = 2x + 3y = 0 \} $)
, donc
 = A $)
?
-
 \not \in \mathbb{R}^2 \backslash \{ (0,0) \} $)
, par définition de la relation d'équivalence
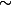
. donc
 \not \in \mathbb{R}^2 / \sim $)
non ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 16:43
par Doraki » 06 Oct 2012, 16:43
P(C²) ? c'est quoi P ?
La relation ~ elle est définie sur R² ou sur R²-{(0,0)} ?? Parceque au début tu parlais de C/~ (R²/~) et là on sait pas trop pourquoi mais tout d'un coup "par définition de ~", {(0,0)} n'est pas une classe d'équivalence de ~ ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 16:48
par barbu23 » 06 Oct 2012, 16:48
Doraki a écrit:P(C²) ? c'est quoi P ?
La relation ~ elle est définie sur R² ou sur R²-{(0,0)} ?? Parceque au début tu parlais de C/~ (R²/~) et là on sait pas trop pourquoi mais tout d'un coup "par définition de ~", {(0,0)} n'est pas une classe d'équivalence de ~ ?

non, dans le cas simplifié que tu proposes; celui sur
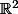
, ( C'est toi qui a choisi l'exemple, pas moi !!! ), la relation d'équivalence, est :
 \} $)
:
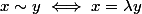
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 17:05
par Doraki » 06 Oct 2012, 17:05
Mais alors pourquoi avant tu parlais de C/~ ?
Enfin bref.
La topologie de P1R est donc la topologie induite par le quotient R²-{(0,0)} -> (R²-{(0,0)})/ ~.
A une droite vectorielle de R², on associe l'élément de (R²-{(0,0)})/~ qui est la classe d'équivalence des générateurs de cette droite. Comme ça t'as le droit de dire que P1R est l'ensemble des droites vectorielles de R².
Ensuite je suis pas au courant de tes notations.
Dans ton U0 = {(x0:x1) de P1R / x0 est non nul}, x0 et x1 sont des réels ? (x0:x1) désigne quelle droite/quelle classe d'équivalence ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 17:13
par barbu23 » 06 Oct 2012, 17:13
Non, on se place dans
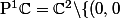 \} / \sim $)
( comme tu as dit au début )
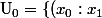 \in P^1 ( \mathbb{C} ) \ / \ x_0 \neq 0 \} $)
Donc :
 \in \mathbb{C}^2 \backslash \{ (0,0) \} $)
.
Voilà, c'est pas grave, on termine. :lol3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 17:35
par Doraki » 06 Oct 2012, 17:35
Ben dans C²/~ il y a la classe {(0,0)}.
Et là juste avant tu disais qu'elle n'existait pas parcequ'on se place dans (C²-{(0,0)})/~.
Il faut savoir.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 17:39
par barbu23 » 06 Oct 2012, 17:39
Voilà, j'ai corrigé ! regarde maintenant !?! :lol3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Oct 2012, 17:43
par Doraki » 06 Oct 2012, 17:43
Ben pour montrer que U0 est un ouvert de P1C il faut donc montrer que ;)-1(U0) est un ouvert de C²-{(0,0)}.
U0 = l'ensemble des classes d'équivalences des éléments (x,y) où x est un complexe non nul et y un complexe quelconque.
Donc c'est quoi ;)-1(U0) comme sous-ensemble de C²-{(0,0)} ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 17:52
par barbu23 » 06 Oct 2012, 17:52
Doraki a écrit:Ben pour montrer que U0 est un ouvert de P1C il faut donc montrer que

-1(U0) est un ouvert de C²-{(0,0)}.
U0 = l'ensemble des classes d'équivalences des éléments (x,y) où x est un complexe non nul et y un complexe quelconque.
Donc c'est quoi

-1(U0) comme sous-ensemble de C²-{(0,0)} ?
 = \Big( \mathbb{C} \backslash \{ 0 \} \Big) \times \mathbb{C} = \mathbb{C}^2 \backslash \{ (0,0 ) \} \bigcap "?" $)
qui est un ouvert de
 \} $)
pour la topologie induite.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 18:07
par barbu23 » 06 Oct 2012, 18:07
Quel est l'inverse de

? :mur:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 19:18
par barbu23 » 06 Oct 2012, 19:18
Un petit coup de main svp. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 20:06
par barbu23 » 06 Oct 2012, 20:06
 = ( 1 : x_1 ) $)
?
 ) = \varphi_{0} ( (1 : x_1 ) ) = \frac{x_{1}}{1} = x_1 $)
 ) ) = \varphi_{0}^{-1} (\frac{x_{1}}{x_{0}} ) = (1 : \frac{x_{1}}{x_{0}} ) = ( x_0 : x_1 ) $)
Correct ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 20:13
par barbu23 » 06 Oct 2012, 20:13
Pourquoi
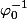
est continue ?
Merci d'avance. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
dans C} où z est dans C²-{(0,0)}.
-1(U0) est un ouvert de C²-{(0,0)}.
-1(U0) comme sous-ensemble de C²-{(0,0)} ?