Besoin d''aide pour trouver un équivalent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cephal
- Membre Naturel
- Messages: 18
- Enregistré le: 09 Sep 2012, 15:24
-
 par Cephal » 29 Sep 2012, 17:58
par Cephal » 29 Sep 2012, 17:58
Bonjour à tous,
je cherche à déterminer un équivalent lorsque n tend vers +inf de sn= Somme(Ln(k), k allant de 1 à n).
Il faut s'aider de l'encadrement:
Pour k>=2, intégrale(ln(x) dx, de k-1 à k)=
Pardon pour la police, qui n'est pas top.
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 29 Sep 2012, 18:04
par BertrandR » 29 Sep 2012, 18:04
Cephal a écrit:Bonjour à tous,
je cherche à déterminer un équivalent lorsque n tend vers +inf de sn= Somme(Ln(k), k allant de 1 à n).
Il faut s'aider de l'encadrement:
Pour k>=2, intégrale(ln(x) dx, de k-1 à k)=<ln(k)=<intégrale(ln(x) dx, de k à k+1)
Pardon pour la police, qui n'est pas top.
En sommant les inégalité de k=2 à n vous devriez être en mesure de faire le calcul des deux encadrants et ainsi obtenir une piste pour l'équivalent
-
Cephal
- Membre Naturel
- Messages: 18
- Enregistré le: 09 Sep 2012, 15:24
-
 par Cephal » 29 Sep 2012, 18:58
par Cephal » 29 Sep 2012, 18:58
Merci pour ton aide BertrandR
J'ai déjà essayer de simplifier par la relation de Chasles des intégrales mais je n'arrive pas à obtenir un encadrement utile pour me permettre de trouver un équivalent.
En effet, je trouve l'inégalité suivante:
intégrale(ln(x) dx, de 1 à n)=< sn=Somme(lnk, k allant de1 à n)=
La première intégrale donne:
- n*(ln(n)-1)+1
- (n+1)*ln(n+1)-2*ln(2)-n+1 ... si mes calculs sont bons.
Et donc, ce que je ne comprend pas c'est que ces deux termes divergent quand on fait tendre n vers +inf.
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 29 Sep 2012, 23:29
par BertrandR » 29 Sep 2012, 23:29
Cephal a écrit:Merci pour ton aide BertrandR
J'ai déjà essayer de simplifier par la relation de Chasles des intégrales mais je n'arrive pas à obtenir un encadrement utile pour me permettre de trouver un équivalent.
En effet, je trouve l'inégalité suivante:
intégrale(ln(x) dx, de 1 à n)=< sn=Somme(lnk, k allant de1 à n)=<intégrale(ln(x) dx, de 2 à n+1)
La première intégrale donne:
- n*(ln(n)-1)+1
- (n+1)*ln(n+1)-2*ln(2)-n+1 ... si mes calculs sont bons.
Et donc, ce que je ne comprend pas c'est que ces deux termes divergent quand on fait tendre n vers +inf.
Rappelle toi de la définition d'un équivalent :
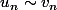
ssi
)
.
Rien n'empêche la divergence. Quels sont les équivalents des deux encadrants ?
-
Cephal
- Membre Naturel
- Messages: 18
- Enregistré le: 09 Sep 2012, 15:24
-
 par Cephal » 30 Sep 2012, 10:07
par Cephal » 30 Sep 2012, 10:07
BertrandR a écrit:Rappelle toi de la définition d'un équivalent :
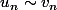
ssi
)
.
Rien n'empêche la divergence. Quels sont les équivalents des deux encadrants ?
Merci encore pour ton aide BertrandR.
Je ne vois vraiment pas comment faire, car ça ne ressemble pas au formes habituelles qu'on transforme en équivalents car ça fait intervenir des sommes et des intégrales, je n'arrive pas à m'en dépatouiller.
Je pense à utiliser la formule de Stirling ln(n!) = somme (ln(k) (
http://fr.wikipedia.org/wiki/Formule_de_Stirling )
-
Cephal
- Membre Naturel
- Messages: 18
- Enregistré le: 09 Sep 2012, 15:24
-
 par Cephal » 30 Sep 2012, 16:41
par Cephal » 30 Sep 2012, 16:41
Ca y est, j'ai réussi à trouver l'équivalent n*(ln (n)), merci pour tes conseils BertrandR
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
ssi
.