Pbl pour trouver un equivalent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ayla8101
- Membre Naturel
- Messages: 38
- Enregistré le: 09 Sep 2006, 21:45
-
 par ayla8101 » 12 Oct 2006, 17:38
par ayla8101 » 12 Oct 2006, 17:38
Bonjour tout le monde,
j'ai un problème pour trouver un equivalent en 0 et +l'infini de cette fonction :
f(x) = (racine de (2+x+x²)) - (racine de (2)) -x.
je me doute qu'il faut utiliser au dvlpt limité de (1+x) mais je n'y arive pas.
SVP aidez moi! Merci
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 12 Oct 2006, 17:59
par tize » 12 Oct 2006, 17:59
multiplie par l'expression conjuguée, tu trouveras des limites...
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 12 Oct 2006, 18:04
par Quidam » 12 Oct 2006, 18:04
ayla8101 a écrit:Bonjour tout le monde,
j'ai un problème pour trouver un equivalent en 0 et +l'infini de cette fonction :
f(x) = (racine de (2+x+x²)) - (racine de (2)) -x.
je me doute qu'il faut utiliser au dvlpt limité de (1+x) mais je n'y arive pas.
SVP aidez moi! Merci
Bonjour,
\times (\sqrt{2+x+x^2}+\sqrt{2}+x)}{\sqrt{2+x+x^2}+\sqrt{2}+x})
-
ayla8101
- Membre Naturel
- Messages: 38
- Enregistré le: 09 Sep 2006, 21:45
-
 par ayla8101 » 12 Oct 2006, 18:11
par ayla8101 » 12 Oct 2006, 18:11
Merci pour vos réponses. Le pbl est que je dois résoudre cet exercice en utilisant les déveoppements limités. Et c'est là que je bloque!
j'ai finalement trouvé la solution en 0, mais j'ai toujours un pbl en l'infini!
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 12 Oct 2006, 18:41
par Quidam » 12 Oct 2006, 18:41
ayla8101 a écrit:Merci pour vos réponses. Le pbl est que je dois résoudre cet exercice en utilisant les déveoppements limités. Et c'est là que je bloque!
j'ai finalement trouvé la solution en 0, mais j'ai toujours un pbl en l'infini!
Dans ce cas, tu peux écrire :
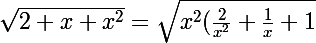}=x \sqrt{\frac{2}{x^2}+\frac{1}{x}+1})
Et après tu fais un développement limité de

.
^n = 1+nk+\frac{n(n-1)}{2} k^2 etc \cdots)
-
ayla8101
- Membre Naturel
- Messages: 38
- Enregistré le: 09 Sep 2006, 21:45
-
 par ayla8101 » 12 Oct 2006, 19:37
par ayla8101 » 12 Oct 2006, 19:37
j'ai fait le développement limité et je trouve à la fin f(x)= (1/x)+(1/2)- racine de 2. Est ce bien le bon résultat? et si oui je conclus que f(x) équivalente à (1/x)?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
