Aide trouver un equivalent

[mohamedjerbi]

soit a>0,n appartient a N*
Un=ln(n)-aln(n+1)+(a-1)ln(n+2)
en a=2 la suite convergente
supposé que a different de 2
a/ecrire DL de ln(1+x) a l'ordre 1 au V 0
ln(1+x)=x+o(x)
b/en déduire Un ~ (a-2)/n
on a ln(x+1)~0 à x
pose u=n-1
n->1
u->0
ln(u+1) ~0 a u => ln(n-1+1) ~1 à n-1

ln(n+1)~0 a n => -aln(n+1)~0 à -an

pose u=n+1
n->-1
u->0
ln(u+1) ~0 a u => ln(n-1+1) ~-1 à n+1
=>(a-1) ln(n-1+1)~-1 à (a-1)(n+1)

le probleme chacun des equivalent tembe ver un Vois different je peut pas faire la somme

[Mimosa]

Bonjour

Tu crois vraiment que tend vers 0 ou vers -1?

Mets en facteur dans chaque logarithme.

[mohamedjerbi]

Bonjour

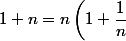Tu crois vraiment que tend vers 0 ou vers -1?

Mets en facteur dans chaque logarithme.

ah oui je fait sa comme c'est un n appartient a R @_@

meme si je fait se que dit resulta
ln(n(1))-aln(n(1+1/2))+(a-1)ln(n(1+2/n))

et si j'additionne les ln:
ln((n.(n+2)^(a-1))/(n+1)^a)

[mohamedjerbi]

ln(n(1))-aln(n(1+1/2))+(a-1)ln(n(1+2/n)) ****

[Mimosa]

Il ne faut pas additionner tout de suite… Je te rappelle que

[mohamedjerbi]

donc
ln(n)-a(ln(n)+ln(1/n))+(a-1)(ln(n)+ln(2/n))

[mohamedjerbi]

meme probleme

[Mimosa]

Et si tu faisais un peu attention?

[mohamedjerbi]

Et si tu faisais un peu attention?

oui mal écrit mais on a le meme problem je peut pas faire un equivalent en un seul voisinage
ln(n)-a(ln(n)+ln(1+1/n))+(a-1)(ln(n)+ln(1+2/n))

[mohamedjerbi]

ah oui
a la fin je trouve -aln(1+1/n)+(a-1)ln(1+2/n)

[Mimosa]

Eh bien ce que tu as écrit vaut



et là tu peux finir tranquillement!

Je dois partir, mais je crois que tu as tout ce qu'il faut.

[mohamedjerbi]

je voit pas comment je peut faire l'equi maintenant

[mohamedjerbi]

Eh bien ce que tu as écrit vaut



et là tu peux finir tranquillement!

Je dois partir, mais je crois que tu as tout ce qu'il faut.

est ce que ca marche lorsque je calcule equivalent en n->+infinie

[mohamedjerbi]

-aln(n+1/n) ~+infinie à -a/n
(a-1)ln(1+2/n)~+infinie à (a-1).2/n
lim Un =lim -aln(1+1/n)+(a-1)ln(1+2/n)=lim (a-2)/n
n->+inf n->+inf n->+inf
donc Un~+inf a-2/2
merci beaucoup

dernier question déduire nature de serie
somme Un n>=1

[mohamedjerbi]

Un tent vers 0 lorsque n tend vers +inf donc c'est une suite convergente vrai?

[pascal16]

limite version taux d'accroissement, moins propre mais suffisante ici :

Un=ln(n)-aln(n+1)+(a-1)ln(n+2)
=2*[ ln(n) - ln(n+2)]/2 + a[ln(n+2)-ln(n+1)]
vaut a peu près
[ ln(n) - ln(n+2)]/2 : on reconnait le taux d'accroissement centré sur ln(n+1), qui vaut environ - ln'(n+1)
je garde aussi une définition centrée pour le second membre

Un ≃ - 2 ln'(n+1) + a ln'(n+1.5)
Un ≃ a/(n+1.5) - 2 / (n+1)
Convergence vers 0 "en (a-2)/n"

[mohamedjerbi]

ok merci