Ensemble de définition

[Shew]

NON !!
(1-x)(1+x) >= 0 n'équivaut pas à 1-x >= 0 ou 1+x >= 0 !!!

(1-x)(1+x) >= 0 équivaut à (1-x >= 0 et 1+x >= 0) ou (1-x <= 0 et 1+x <= 0)
(Un produit est positif si les 2 facteurs sont de même signe)
D'où l'intérêt du tableau de signes pour synthétiser les résultats.

????????? Cela n'a aucun interet surtout avec une fonction racine carrée , la deuxieme partie serait inutile .

[titine]

????????? Cela n'a aucun interet surtout avec une fonction racine carrée , la deuxieme partie serait inutile .

Que veux tu dire ?
Il est vrai qu'on ne peut pas avoir 1-x =1 et x = 0 n'équivaut pas à 1-x >= 0 ou 1+x >= 0

[Shew]

Que veux tu dire ?
Il est vrai qu'on ne peut pas avoir 1-x =1 et x = 0 n'équivaut pas à 1-x >= 0 ou 1+x >= 0

Si je suis votre raisonnement si

alors pour et

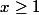
Nous aurions alors et

Essayons maintenant avec une valeur plus grande que 1 , par exemple 2 soit

soit = n'est pas

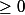
Essayons avec une valeur inferieur a -1 soit -3

= qui n'est pas

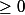
Cela demontre que votre raisonnement est faux .

Si c'est le ou qui vous embete , ce n'est rien c'est juste un probleme de formatage de texte , on mettra et parce qu'en effet l'un des deux facteurs ne peut pas être negatif .

[Iroh]

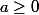
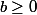
Salut, si et sont deux nombres réels, alors ssi et sont de même signe, càd qu'il sont soit tous les deux positifs, soit négatifs. Donc ssi (( et ) ou ( et ))

[Shew]

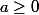
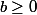
Salut, si et sont deux nombres réels, alors ssi et sont de même signe, càd qu'il sont soit tous les deux positifs, soit négatifs. Donc ssi (( et ) ou ( et ))

Vue ainsi , en effet .

[titine]

Oui c'est exactement ce que j'ai dit !

Attention Shew au confusion entre et et ou

Par exemple pour f :
f(x) = rac(x²-1)
f définie lorsque x²-1 =(x-1)(x+1) >= 0
C'est à dire
lorsque x-1 >= 0 et x+1 >= 0 c'est à dire lorsque x appartient à [1 ; +inf[
ou
orsque x-1 <= 0 et x+1 <= 0 c'est à dire lorsque x appartient à ]-inf ; -1]

[Shew]

Oui c'est exactement ce que j'ai dit !

Attention Shew au confusion entre et et ou

Par exemple pour f :
f(x) = rac(x²-1)
f définie lorsque x²-1 =(x-1)(x+1) >= 0
C'est à dire
lorsque x-1 >= 0 et x+1 >= 0 c'est à dire lorsque x appartient à [1 ; +inf[
ou
orsque x-1 <= 0 et x+1 <= 0 c'est à dire lorsque x appartient à ]-inf ; -1]

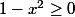
Dans ce cas precis je mets une reserve sur l'utilisation du et car dans une inequation comme , ne peut prendre qu'une seule valeur a la fois . On peut le verifier en resolvant directement l'inequation . De plus vous pouvez verifier la fonction en la traçant dans un repere , vous constaterez alors que l'encadrement correspond a ce que j'ai mis dans mon commentaire plus haut .

[titine]

Dans ce cas precis je mets une reserve sur l'utilisation du et car dans une inequation comme , ne peut prendre qu'une seule valeur a la fois .

Je ne comprends pas vraiment ce que tu veux dire.
On a bien toujours :

J'insiste lourdement, lorsque tu écris :

ou

Cela est FAUX.

On peut le verifier en resolvant directement l'inequation .

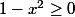
Que veux tu dire par : "résoudre directement l'inéquation " ?
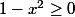
Il est vrai qu'on peut dire que 1 - x² >= 0 revient à x² <= 1 et que, connaissant le comportement de la fonction carré, cela est vérifié lorsque -1 <= x <= 1

De plus vous pouvez verifier la fonction en la traçant dans un repere , vous constaterez alors que l'encadrement correspond a ce que j'ai mis dans mon commentaire plus haut .

Ton résultat est juste mais ton raisonnement est faux ! (Voir ci dessus)

De manière général, la meilleur manière d'étudier le signe d'un produit s'est d'utiliser un tableau de signes. Ça évite bien des erreurs.

[Shew]

Ca y'est j'ai compris le sens de et dans cette perspective (sorti du contexte booleen) . C'est bon titine vous avez raison