Bonsoir
Dans un problème on se propose de montrer que le polynôme
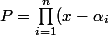 -1)
est irréductible dans

avec les
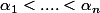
des entiers relatifs.
J'avoue que je trouve des difficultés pour résoudre cette question ; voici les pistes de réflexion que j'ai essayé :
j'ai supposé par l'absurde que
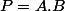
avec A et B appartiennent à Z[X]. On a alors
B(\alpha _k) = -1)
avec
 et B(\alpha _k) dans \mathbb{Z})
. On alors l'une des deux possibilités : soit
 = 1 et B(\alpha _k)=-1)
soit l'inverse. Si on suppose que
 = 1)
alors le polynôme A - 1 admet n racines (en occurrence les
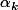
) et donc
=deg(A+1) \geq n)
ce qui est absurde. Ainsi, il y a des racines pour lesquelles
 = 1)
et d'autres pour lesquelles
 = -1)
. Si on note

le sous-ensemble de
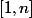
pour lequel
 = 1)
. On a alors immédiatement les résultats suivants :
 divise A-1 et B + 1)
et
 divise A+1 et B-1)
. Si on note

le cardinal de I on a
)
et
)
puisque les
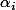
sont distincts par le théorème de Gauss
)
divise
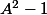
On obtient donc
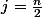
(en raisonnant par l'absurde) et
 = deg (B)=\frac{n}{2})
et
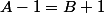
Après j'avoue que je bloque pour conclure (le cas de n impair est déjà résolu )
Si quelqu'un peut me donner un coup de main
