Démonstrations par récurences sur suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 01 Jan 2011, 20:47
par wako » 01 Jan 2011, 20:47
Bonjour, je me tourne à nouveau vers vous pour m'aider à répondre à deux questions différentes :
1- Soit la suite :
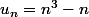
Comment prouver par récurrence que les valeurs de cette suite sont multiples de 3 ?
2- Soit la suite
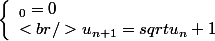
Comment prouver par qu'elle est majorée par
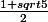
?
Puis qu'elle est minorée ?
Merci pour vos réponses ! et bonne année
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 01 Jan 2011, 21:03
par XENSECP » 01 Jan 2011, 21:03
Tu supposes que
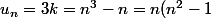 = n(n+1)(n-1))
.
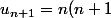(n+2) = n(n+1)(n-1+3) = n(n+1)(n-1) + 3n(n+1))
Je te laisse conclure.
Pour la 2) il s'agit du point fixe
 = \sqrt{x+1} = x)
Et comme elle est croissante... Toute suite croissante est minorée par son premier terme.
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 01 Jan 2011, 23:21
par wako » 01 Jan 2011, 23:21
Merci pour ces réponses éclairs !
Alors pour le 1 je suis ok, même si un peu dégouté puisque j'avais la bonne méthode, je suis arrivé au même terme pour

, c'est juste le coup du n +1 = n-1+3 que je n'avais pas vu et que je considère un petit peu "borderline" ou mesquin plutôt ... :mur:
par contre pour le 2 , désolé je ne sais pas ce qu'est le point fixe, du coup je n'ai rien compris ...
Merci en tous cas !
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 01 Jan 2011, 23:25
par XENSECP » 01 Jan 2011, 23:25
Lol, c'est la petite astuce sympa

Pour la 2), tu n'as pas vu les suites définies par une fonction ?
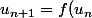)
Il y a des particularités à ce type de suites. S'il existe un point fixe (f(x) = x), alors la suite va converger vers ce point.
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 02 Jan 2011, 11:26
par wako » 02 Jan 2011, 11:26
Pour tout dire je n'ai pas de cours du tout, puisque je me sers de mes souvenirs datant de 12 ans ... Bon sinon j'ai compris le coup du pont fixe. Effectivement si on ne le connait pas on risque d'avoir des problèmes pour répondre...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Jan 2011, 16:08
par Sa Majesté » 02 Jan 2011, 16:08
Pour la 1 tu n'as pas d'astuce à utiliser
Tu montres que

est multiple de 3
Tu supposes que
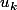
est multiple de 3
Alors
^3 - (k+1) = k^3 - k + 3k^2 + 3k = u_k + 3(k^2+k))
est multiple de 3
Utiliser
n(n+1))
sert uniquement pour la preuve directe sans récurrence
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Jan 2011, 18:17
par XENSECP » 02 Jan 2011, 18:17
Sa Majesté a écrit:Pour la 1 tu n'as pas d'astuce à utiliser
Tu montres que

est multiple de 3
Tu supposes que
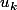
est multiple de 3
Alors
^3 - (k+1) = k^3 - k + 3k^2 + 3k = u_k + 3(k^2+k))
est multiple de 3
Utiliser
n(n+1))
sert uniquement pour la preuve directe sans récurrence
Vu qu'il faut déjà faire une récurrence après, je me suis dis que la "preuve directe" était pas mal

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
est multiple de 3
est multiple de 3
est multiple de 3
sert uniquement pour la preuve directe sans récurrence