Demonstrations sur les suites

[Anonyme]

Bonjour j'ai un problème pour ces démonstrations.

Montrer si la proposition est vrai ou fausse.

Deux suites (un) et (vn) sont définies pour tout entier naturel non nul n par les relations :
un = (1/n)+(1/n+1)+...+(1/2n) et vn = (1/n+1)+(1/n+2)+...+(1/2n)

A] Les suites (un) et (vn) sont toutes les deux croissantes.

B] u3=19/20 et v3= 37/60

C] les suites ( un ) et (vn) ne sont pas majorées.

D] Les suites (un) et (vn) sont adjacentes.

J'ai un problème pour les questions B C D
Pour le A] j'ai utiliser (un+1)-un et c'est une proposition fausse.
Merci d'avance.

[Sa Majesté]

Bonjour,
Pour le A) combien trouves-tu pour u(n+1)-u(n) ?

[Anonyme]

Désolé du retard.
Pour le A], j'ai trouver que c'était faux.

(un+1)-(un) = 1/(2n) - 1/n < 0
Donc (un) decroissante.

(vn+1)-(un) = 1/(2n+2) - 1/(n+1) < 0
Donc (vn) decroissante.

Mais j'arrive toujours pas le reste :triste:

[Sa Majesté]

(un+1)-(un) = 1/(2n) - 1/n < 0
Donc (un) decroissante.

(vn+1)-(un) = 1/(2n+2) - 1/(n+1) < 0
Donc (vn) decroissante.

J'ai des doutes sur tes calculs
u(n+1) = 1/(n+1)+1/(n+2)+...+1/(2(n+1))
ou alors j'ai rien compris ?

[Anonyme]

Oui c'est ca que j'ai fais.

(un+1) - (un) = ((n+1)+(1/n+2) + .. +(1/(2n+2)) - ((1/n)+(1/n+1) + ... + (1/2n)
= (1/(2n+2)) -(1/n) < 0 car 2n+2>n

Donc la suite (un) est decroissante.

Voilà ce que j'ai écrit. mais peut etre qu'il y a un erreur de calcul.

[Sa Majesté]

Je pense qu'il y a une erreur
u(n) s'arrête à 1/(2n)
u(n+1) s'arrête à 1/(2n+2)
donc qd tu fais la différence il reste 1/(2n+2) mais aussi 1/(2n+1)

[Anonyme]

donc sa fais u(n+1) - un = 1/(2n+2)- ( 1/n + 1/2n) .
Mais c toujours decroissant ... car 1/(2n+2) < (2n+n)/(2n)^2)

[Sa Majesté]

Non ça fait
u(n+1)-u(n)=1/(2n+2)+1/(2n+1)-1/n
Sauf erreur de ma part

[Anonyme]

Je crois que tu as faux. J'ai refait mon calcul et c'est le bon.

[Anonyme]

???? de l'aide

[tigre]

donc


continue

[Anonyme]

c'est un+1-un qui faut faire et pas un-un+1 je pense ...

[tigre]

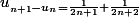
continue :briques: oui voila

[Anonyme]

Vous pourriez me faire le développement svp. Je comprend pas comment on passe de un+1 - un à (1/2n+1) + (1/2n+2 )

[tigre]

=
=
j'espére que moi aussi en m'aidera pour mon exersice

[Sa Majesté]

Je ne suis pas d'accord avec le k=0 pour u(n+1)
u(n+1) commence à 1/(n+1)

[tigre]

bien vu votre Majesté