Bon, en partant de la fin :
Le 3), C'est ok sauf le "...Et en simplifiant j'ai trouvé 1/2 !!" qui normalement, devrait être un "...Et en simplifiant j'ai trouvé
un truc qui tend vers 1/2 !!"
Pour la fin du 2), il faut effetcivement écrire que
^3}{6} \leq sin(\frac{1}{n^2}))
mais, dans le terme da gauche, la seule simplification que tu fait, c'est d'écrire que
^3}{6} =\frac{1}{n^2}-\frac{1}{6 n^6})
mais il ne faut
surtout pas réduire au même dénominateur car le
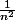
est le "début" de Vn et il faut le garder "tel quel".
Ce qu'il faut faire, c'est comme au 1), c'est à dire écrire conciencieusement
)
(déjà fait) puis
)
puis
)
puis . . . puis
)
puis ajouter toutes les inégalités pour avoir un truc du genre

et,
si tu n'as pas réduit au même dénominateur, dans les "..." il va y avoir ton Vn. Il ne restera plus qu'à minorer ce que tu as dans le "..." et qui "n'est pas du Vn"...
Pour le début du 2), c'est... un peu n'importe quoi...
Pour l'hérédité, tu suppose que, pour un certain n>=1 tu as bien 1^3+2^3+...+n^3=<n^4 (*)
et il faut que tu montre que 1^3+2^3+...+n^3+(n+1)^3=<(n+1)^4
Evidement, on déduit de l'hypothése de réccurence (*) que
1^3+2^3+...+(n+1)^3 = (1^3+2^3+...+n^3) + (n+1)^3 =< n^4 +(n+1)^3
donc il suffit de montrer que n^4 +(n+1)^3 =< (n+1)^4.
Pour montrer cette formule qui ne contient pas de points de suspension,
il ne faut pas faire une réccurence, mais simplement écrire qu'elle équivaut à n^4 =< (n+1)^4 - (n+1)^3, c'est à dire à n^4 =< (n+1)^3[(n+1)-1] et donc à n^4 =< n(n+1)^3 ce qui est évidement vrai.
