Trouver tous les polynomes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 25 Déc 2010, 20:45
par cheria2010 » 25 Déc 2010, 20:45
Trouver tous les polynômes

définies sur

tel que:
=1)
et
-P(x)=2P'(x)+1)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Déc 2010, 22:33
par girdav » 25 Déc 2010, 22:33
Si

est solution avec
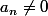
et

alors
-P(x) = a_n(nx^{n-1}+\sum_{k=0}^{n-2}\binom{n}{k} x^k)+\mbox{termes de deg}\leq n-2)
et
 +1 = 2na_nx^{n-1} +\mbox{termes de deg}\leq n-2)
donc
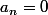
et c'est une contradiction.
Il ne reste donc qu'à regarder pour les polynômes de degré inférieur à

.
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 26 Déc 2010, 13:25
par cheria2010 » 26 Déc 2010, 13:25
salut tout le monde
pourquoi
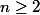
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 14:00
par girdav » 26 Déc 2010, 14:00
Comme il apparait des termes de degré
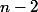
, il faut que

.
On peut trouver les polynômes de degré inférieur à

qui marchent : si
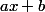
,

alors
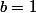
et
-P(x) = a = 2a+1)
donc
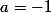
et
 =-x+1)
.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 14:04
par girdav » 26 Déc 2010, 14:04
Sinon, on pouvait procéder comme ça : si un polynôme de degré

supérieur à

convient, alors en posant
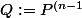})
on voit que Q est de degré

et satisfait à
-Q(X)=2Q'(X))
(car le fait que

nous a obligé à dériver au moins une fois) ce qui ne va pas.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Déc 2010, 14:17
par Nightmare » 26 Déc 2010, 14:17
Hello,
autre méthode : Appliquer la formule de taylor pour les polynômes
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 26 Déc 2010, 16:16
par cheria2010 » 26 Déc 2010, 16:16
merci c'est un bon travail...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
