Cardinalite de tous les parties finis de N

par **badola** » 07 Déc 2008, 17:54

J'ai lu sur Wikipedia que la cardinalité d'un ensemble de parties de

ne pouvait être que finie, dénombrable, ou celle de

.

Je pense que la cardinalité de la classe des sous-ensembles finis de

est infini dénombrable donc a meme cardinal que

.
Pour montrer qu'elle ne peut être finie est triviale, mais j'ai pas reussi qu'on ne peut avoir une bijection entre la classe des sous-ensembles finis de

et

.

par **Arkhnor** » 07 Déc 2008, 18:01

Bonjour.

Tu peux dire que pour n fixé, l'ensemble des parties de

à n éléments est dénombrable (on peut l'injecter dans

), et ensuite remarquer que l'ensemble que tu considères s'écrit comme la réunion des ensembles des parties à n éléments, pour

.
C'est une réunion dénombrable d'ensembles dénombrables, donc l'ensemble des parties finies de

est dénombrable.

par **yos** » 07 Déc 2008, 18:10

Arkhnor a écrit:l'ensemble des parties de est dénombrable.

Non, il y a plus de parties que d'éléments, c'est bien connu. Et c'est pas seulement pour N. C'est vrai aussi pour R, et même pour l'ensemble vide.

par **yos** » 07 Déc 2008, 18:13

Arkhnor a écrit:ensuite remarquer que l'ensemble que tu considères s'écrit comme la réunion des ensembles des parties à n éléments, pour .
C'est une réunion dénombrable d'ensembles dénombrables, donc l'ensemble des parties de est dénombrable.

Tu comptes bien, ... sauf pour les parties infinies.

par **lapras** » 07 Déc 2008, 18:19

Salut
notons

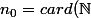alors le cardinal de l'ensemble des parties de

est

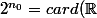Donc si on prend en compte les parties infinies, l'ebsemble des parties de

n'est pas dénombrable.

par **Imod** » 07 Déc 2008, 18:31

Un des plus beau résultat de Cantor Card(E)
Imod

par **Arkhnor** » 07 Déc 2008, 19:09

C'est une réunion dénombrable d'ensembles dénombrables, donc l'ensemble des parties de est dénombrable.

J'ai oublié le mot "finies" dans ma phrase. Mea culpa. :wrong:
Evidemment que l'ensemble des parties de

est indénombrable. Je répondais à la question du message initial, sur les parties finies de

.
Encore désolé.

par **skilveg** » 07 Déc 2008, 19:18

@ badola: est-ce que ça suppose l'hypothèse du continu, ou est-ce que c'est prouvé sans hypothèse?

par **Luc** » 07 Déc 2008, 19:25

lapras a écrit:Salut
notons
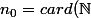alors le cardinal de l'ensemble des parties de est
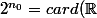Donc si on prend en compte les parties infinies, l'ebsemble des parties de n'est pas dénombrable.

Salut,

Effectivement si

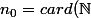alors le cardinal de l'ensemble des parties de

est

.

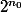
Par contre pour dire que

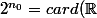, je ne connais pas de preuve qui ne fait pas appel à l'hypothèse du continu. (qui énonce :toute partie infinie de

est équipotente à

ou

).

L'hypothèse du continu est indépendante des axiomes de la théorie des ensembles ZFC (Zermelo-Fraenkel + axiome du choix) , ou encore indécidable dans cette théorie. (Gödel, 1938).

La recherche d'hypothèses naturelles à ajouter à la théorie ZFC et d'arguments qui permettraient de trancher pour ou contre l'hypothèse du continu constitue toujours un sujet actif en théorie des ensembles.

Cordialement,

Luc

par **Luc** » 07 Déc 2008, 19:28

skilveg a écrit:@ badola: est-ce que ça suppose l'hypothèse du continu, ou est-ce que c'est prouvé sans hypothèse?

Pas besoin de l'hypothèse du continu grâce à la preuve d'Arkhnor: l'ensemble des parties finies de

est une union dénombrable de dénombrables (les parties finies à

éléments). Il est donc dénombrable.

Cordialement,

Luc

par **Arkhnor** » 07 Déc 2008, 19:30

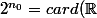Par contre pour dire que , je ne connais pas de preuve qui ne fait pas appel à l'hypothèse du continu.

Il me semblait que c'était un fait démontré sans utiliser l'hypothèse du continu, en utilisant des développements en base 3.
C'est l'affirmation

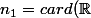, où

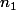
désigne le plus petit cardinal strictement supérieur à

qui est en rapport avec l'hypothèse du continu.

Enfin, c'est sous réserve, j'ai assez dit de bêtises pour aujourd'hui ...

par **Luc** » 07 Déc 2008, 19:49

Arkhnor a écrit:Il me semblait que c'était un fait démontré sans utiliser l'hypothèse du continu, en utilisant des développements en base 3.
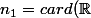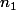
C'est l'affirmation , où désigne le plus petit cardinal strictement supérieur à qui est en rapport avec l'hypothèse du continu.

Enfin, c'est sous réserve, j'ai assez dit de bêtises pour aujourd'hui ...

La seul preuve que je connaisse utilise l'injectivité de la fonction qui à une partie A de N associe un nombre réel d'écriture décimale illimitée

où

si

et

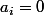
sinon. Du coup,

est équipotent à une partie infinie de

. On conclut avec l'hypothèse du continu (puisque

n'est pas dénombrable).

Je suis curieux de savoir s'il existe d'autres preuves que

est équipotent à

, qui ne font pas appel à l'hypothèse du continu.

Luc

par **Arkhnor** » 07 Déc 2008, 19:56

Là on a construit une injection de P(N) dans R, on construit ensuite une injection de R dans P(N), et on conclut avec Cantor-Bernstein.

Je pose g l'application de ]0,1[ dans P(N) définie par g(x) = {ensemble des entiers naturels n tels que le n-ième chiffre dans le développement de x est 1}

C'est un injection, par unicité du développement binaire (en ayant par convention exclu les développements stationnaires à 0 à partir d'un certain rang)

Sauf erreur.

par **badola** » 07 Déc 2008, 19:57

Je suppose l'hypothese du continu. C'est pourquoi, j'ai tenter de prouver qu'on ne peut pas avoir une bijection entre l'ensemble des parties finies de

et

.
L'idee de Arkhnor est rapide et facile.
C'est ce qu'on aime de faire en Maths. N'est-ce pas?

par **ThSQ** » 07 Déc 2008, 19:58

Le fait que |R| = P(N) ne dépend pas de l'hypothèse du continu (ni de l'Axiome du Choix). On peut injecter l'un dans l'autre et on conclut avec Cantor-Berstein

par **mathelot** » 07 Déc 2008, 21:45

Cantor-Bernstein

par **Luc** » 08 Déc 2008, 12:31

ThSQ a écrit:Le fait que |R| = P(N) ne dépend pas de l'hypothèse du continu (ni de l'Axiome du Choix). On peut injecter l'un dans l'autre et on conclut avec Cantor-Berstein

Voilà la réponse que j'attendais

Merci!

Luc

par **Luc** » 08 Déc 2008, 12:32

badola a écrit:Je suppose l'hypothese du continu. C'est pourquoi, j'ai tenter de prouver qu'on ne peut pas avoir une bijection entre l'ensemble des parties finies de et .

Relis sa démonstration, tu n'as pas besoin de l'hypothèse du continu (ni même du fait que

est équipotent à

)

Luc

par **Luc** » 08 Déc 2008, 12:37

Arkhnor a écrit:Là on a construit une injection de P(N) dans R, on construit ensuite une injection de R dans P(N), et on conclut avec Cantor-Bernstein.

Je pose g l'application de ]0,1[ dans P(N) définie par g(x) = {ensemble des entiers naturels n tels que le n-ième chiffre dans le développement binaire de x est 1}

C'est un injection, par unicité du développement binaire (en ayant par convention exclu les développements stationnaires à 0 à partir d'un certain rang)

Sauf erreur.

Je suis d'accord: les réels de ]0,1[ qui possèdent deux développement binaires distincts étant en nombre au plus dénombrable, on peut conclure que R s'injecte dans P(N).

Merci!

Luc

Cardinalite de tous les parties finis de N

Cardinalite de tous les parties finis de N

Qui est en ligne