Trouver tous les entiers n

par **cheria2010** » 03 Nov 2011, 14:14

salut tout le monde

ma question est de trouver tous les entier n tel que :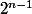

devise

par **Skullkid** » 03 Nov 2011, 15:49

Bonjour, n! est un produit d'entiers. Parmi ces entiers, quels sont ceux qui vont contribuer à la divisibilité par 2 de n! ? Combien sont ces entiers ?

par **cheria2010** » 03 Nov 2011, 19:55

Skullkid a écrit:Bonjour, n! est un produit d'entiers. Parmi ces entiers, quels sont ceux qui vont contribuer à la divisibilité par 2 de n! ? Combien sont ces entiers ?

salut

il y a au plus (n-2)/2 entiers pairs .mais parmi ces entiers on trouve des facteurs de la forme:

il faut les compter.

par **Skullkid** » 03 Nov 2011, 19:59

cheria2010 a écrit:il y a au plus (n-2)/2 entiers pairs .

Non, par exemple dans {1,2} il y a un entier pair, ce qui est strictement plus que (2-2)/2. J'aimerais que tu me donnes le nombre exact, en fonction de n, d'entiers pairs dans |[1,n]|.

cheria2010 a écrit:mais parmi ces entiers on trouve des facteurs de la forme:
il faut les compter.

C'est vrai, mais une chose à la fois.

par **cheria2010** » 03 Nov 2011, 20:29

salut
pour n pair : comptons de 2 à n ; il ya n/2
pour n impair il y a (n-1)/2

par **Skullkid** » 03 Nov 2011, 20:35

Voilà, ce qui peut s'écrire de façon plus unifiée [n/2], avec [.] la fonction partie entière.

Maintenant, comme tu l'as fait remarquer, certains nombres pairs ne font pas sortir qu'un seul 2. Par exemple, 12 en fait sortir 2, puisque 12 = 3*2².

Quels sont les nombres qui font sortir au moins k facteurs 2 ? Combien y en a-t-il ? Quel est l'exposant de 2 dans la décomposition en facteurs premiers de n! ?

par **cheria2010** » 04 Nov 2011, 20:24

Skullkid a écrit:Voilà, ce qui peut s'écrire de façon plus unifiée [n/2], avec [.] la fonction partie entière.

Maintenant, comme tu l'as fait remarquer, certains nombres pairs ne font pas sortir qu'un seul 2. Par exemple, 12 en fait sortir 2, puisque 12 = 3*2².

Quels sont les nombres qui font sortir au moins k facteurs 2 ? Combien y en a-t-il ? Quel est l'exposant de 2 dans la décomposition en facteurs premiers de n! ?

salut
j'ai pas trouver de formule generale pour ca
n=12 ,

n=8 ,

alors 8 solution et 12 non
a vous

par **Skullkid** » 04 Nov 2011, 20:27

Ok, alors on va y aller plus lentement.

Ça se traduit comment qu'un entier de |[1,n]| fait sortir au moins 2 facteurs 2 dans la décomposition de n! ? Combien y a-t-il de tels entiers ?

Trouver tous les entiers n

Trouver tous les entiers n

Qui est en ligne