Nombres complexes:
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 28 Nov 2010, 18:38
par Anonyme » 28 Nov 2010, 18:38
Tu trouve pas que :

on un facteur commun non nul?
-
slavik
- Membre Relatif
- Messages: 194
- Enregistré le: 07 Mar 2010, 10:51
-
 par slavik » 28 Nov 2010, 18:39
par slavik » 28 Nov 2010, 18:39
z n'est pas égal à 1, ce qui permet de simplifier par...
là je sais pas ...
-
slavik
- Membre Relatif
- Messages: 194
- Enregistré le: 07 Mar 2010, 10:51
-
 par slavik » 28 Nov 2010, 18:41
par slavik » 28 Nov 2010, 18:41
Qmath a écrit:Tu trouve pas que :

on un facteur commun non nul?
Pff je comprends vraiment rien

J'arrive pas a saisir le truc des opérations sur les modules...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 28 Nov 2010, 18:41
par Nightmare » 28 Nov 2010, 18:41
Eh bien, par 1-z !
-
Anonyme
 par Anonyme » 28 Nov 2010, 18:48
par Anonyme » 28 Nov 2010, 18:48
-
slavik
- Membre Relatif
- Messages: 194
- Enregistré le: 07 Mar 2010, 10:51
-
 par slavik » 28 Nov 2010, 18:48
par slavik » 28 Nov 2010, 18:48
Nightmare a écrit:Eh bien, par 1-z !
Par |1-z|² non?
Et on peut faire ca car |z|=|z(bar)|
donc: |z²-1|=|z²+1|
-
Anonyme
 par Anonyme » 28 Nov 2010, 18:52
par Anonyme » 28 Nov 2010, 18:52
Apres pour les modules

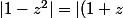(1-z)|=|(1+z)||(1-z)|)
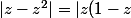|=|z||(1-z)|)
Donc:
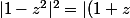|^2|(1-z)|^2)
et
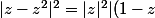|^2)
tu comprends mieux ?
-
slavik
- Membre Relatif
- Messages: 194
- Enregistré le: 07 Mar 2010, 10:51
-
 par slavik » 28 Nov 2010, 19:02
par slavik » 28 Nov 2010, 19:02
Qmath a écrit:Apres pour les modules

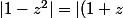(1-z)|=|(1+z)||(1-z)|)
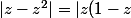|=|z||(1-z)|)
Donc:
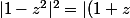|^2|(1-z)|^2)
et
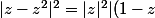|^2)
tu comprends mieux ?
Oui oui, plus ou moins.
ensuite il faut démontrer que cette écriture équivaut à
(z+(1/2))((z+(1/2))bar)=(1/4)
Là je ne vois pas non plus vraiment comment on fait non plus =(
Qu'est ce que vous me conseilleriez de revoir pour ne pas rester bloquer devant de tels exercices?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
