Croissance par récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 14 Nov 2010, 17:56
par nodjim » 14 Nov 2010, 17:56
u(n+1)=V(un+1)
Comparons u et V(u+1)
uV(u+1)
u²u+1 l'équivalence est vraie car u>0 car u0>0 et donc la suite > 0.
u²-u-10
Résoudre et discuter.
-
Lechero
- Membre Naturel
- Messages: 78
- Enregistré le: 18 Sep 2010, 11:11
-
 par Lechero » 14 Nov 2010, 18:00
par Lechero » 14 Nov 2010, 18:00
Désolé, mais pas compris nodjim.
Je vais essayer de faire ce qui est marqué au dessus avec n

1 car l'inégalité est stricte.
-
Lechero
- Membre Naturel
- Messages: 78
- Enregistré le: 18 Sep 2010, 11:11
-
 par Lechero » 14 Nov 2010, 18:29
par Lechero » 14 Nov 2010, 18:29
Bon, rien a faire, j'y arrive pas du tout du tout ...
Initialisat° => Ok (seulement pour n > 1)
Hérédité => Ok
[...]
On a Up - 3 <
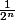
Et là, rien, nada, le vide ...
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 14 Nov 2010, 18:32
par Mortelune » 14 Nov 2010, 18:32
Je t'avais presque fini l'hérédité, ton vide commence où ?
-
Lechero
- Membre Naturel
- Messages: 78
- Enregistré le: 18 Sep 2010, 11:11
-
 par Lechero » 14 Nov 2010, 18:36
par Lechero » 14 Nov 2010, 18:36
Je suis vraiment désolé...
Je bloque au moment où, dans l'hérédité, on doit passer :
Up - 3 <

à Up+1 - 3 <

-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 14 Nov 2010, 18:43
par Mortelune » 14 Nov 2010, 18:43
C'est normal que ce soit plus dur c'est ce qu'il faut montrer.
Donc tu n'as toujours pas montré l'inégalité de Ben ni compris comment je l'avais utilisée ?
-
Lechero
- Membre Naturel
- Messages: 78
- Enregistré le: 18 Sep 2010, 11:11
-
 par Lechero » 14 Nov 2010, 18:51
par Lechero » 14 Nov 2010, 18:51
Non ... :mur:
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 14 Nov 2010, 18:56
par Mortelune » 14 Nov 2010, 18:56
Alors déjà même si tu ne vois pas encore à quoi elle sert tu peux la montrer ce sera fait.
Ensuite pour ça :
 \leq \frac{1}{2}.\frac{1}{2^n})
On va le décomposer
)
ça c'est l'inégalité de Ben.

ça c'est ton hypothèse de récurrence.
Si on multiplie la 2e ligne par

On a alors :
 \leq \frac{1}{2}.\frac{1}{2^n})
donc
 \leq \frac{1}{2^{n+1}})
Ce qu'on peut réintroduire dans l'inégalité de Ben pour obtenir l'hérédité.
-
Lechero
- Membre Naturel
- Messages: 78
- Enregistré le: 18 Sep 2010, 11:11
-
 par Lechero » 14 Nov 2010, 19:03
par Lechero » 14 Nov 2010, 19:03
Mortelune a écrit:Alors déjà même si tu ne vois pas encore à quoi elle sert tu peux la montrer ce sera fait.
Justement, c'est ça le hic ^^
Mais je pense que vous m'avez déjà assez aidé, et je voudrais pas vous embêter encore plus.
Je tiens à vous remercier énormément, vous êtes vraiment sympa ! =)
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 14 Nov 2010, 19:10
par Mortelune » 14 Nov 2010, 19:10
Dans ta démonstration tu dois faire apparaitre un 1/2, alors prend celui de Un+1 et mets le en facteur devant tout ce qui revient à majorer ce qu'il reste par 1, donc par exemple faire apparaitre un 1 moins quelque chose compris entre 0 et 1.
-
Lechero
- Membre Naturel
- Messages: 78
- Enregistré le: 18 Sep 2010, 11:11
-
 par Lechero » 14 Nov 2010, 20:19
par Lechero » 14 Nov 2010, 20:19
A partir de Un - 3 < 1/2^n, je ne sais rien faire, la puissance au dénominateur m'embrouille, donc voilà ...
Je ne suis arrivé qu'à ça :
 < \frac{1}{2^{n+1}})

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
 \leq \frac{1}{2}.\frac{1}{2^n})
) ça c'est l'inégalité de Ben.
ça c'est l'inégalité de Ben. ça c'est ton hypothèse de récurrence.
ça c'est ton hypothèse de récurrence.
 \leq \frac{1}{2}.\frac{1}{2^n}) donc
donc  \leq \frac{1}{2^{n+1}})
