Croissance par récurrence

[Lechero]

bonjour à tous,

je bloque sur un exercice de révisions, j'aimerais que vous m'aidiez s'il vous plait

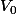
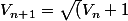On me demande de démontrer par récurrence que la suite (Vn) est croissante. J'ai = 1 et Je dois en déduire que la suite converge et donner sa limite.

J'ai préalablement démonter que 1 < Vn < 2 et que la, fonction f(x) = était croissante sur R+.

Merci d'avance !

[Mortelune]

Bonjour.

Oui tu peux le démontrer par récurrence, l'initialisation est presque immédiate, il suffit d'exprimer .

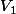
Pour l'hérédité on a et en appliquant une fonction croissante que tu as défini au dessus on s'en sort.

[Lechero]

Vn-1 ? On ne doit pas utiliser plutôt le rang p+2 dans l'hérédité ?

Et comment peut-on exprimer V1 ?

Merci pour la réponse en tout cas !=)

[Mortelune]

1 c'est 0+1 quand n=0, la suite est définie par son premier terme et les autres termes sont définis par récurrence.

Pour l'hérédité tu la fait avec le rang n que tu veux, l'essentiel est de montrer que c'est vrai pour le rang suivant.

[Lechero]

Doc initialisation : V0 = 1 et 1 (= V1 = )

Hérédité:

Soit p un entier naturel tel que la propriété est vraie au rang p, soit Vp < Vp+1
Montrons qu'alors la propriété est vrai au rang p+1, soit : Vp+1 < Vp+2

On a :
Vp < Vp+1

et là je ne sais pas comment appliquer f(x) en fait.... (je sais néanmoins que l'ordre ne sera pas modifié car f est croissante sur N)

[Mortelune]

C'est ça mais tu as f(Vp)= ...

[Lechero]

Initialisation : ...
Hérédité: ...

On a:
Vp < Vp+1

La fonction f est f(x)= et est croissante, donc :

<

Soit:
Vp+1 < Vp+2

On montre ainsi, avec l'axiome de récurrence, que pour tout n appartient à N, Un< Un+1; la suite est donc croissante.

Merci !

Mais désormais, comment en déduire qu'elle converge et quelle est sa limite ?
(suite croissante donc converge vers son majorant ? quel est-il ?) ...

[ffpower]

Oui, suite croissante et majorée donc convergente. Après tu notes l la limite, et tu fais tendre n vers l'infini dans la relation

[Lechero]

Elle est croissante, ça oui, mais comment savoir qu'elle est majorée ?

De plus, pour la limite, je pense que c'est +infini, mais comment le démontrer avec Vn+1 ?
En disant que lim x+1 = +infini et que lim = +inf donc que lim = +infini ?

[Mortelune]

Attention, une suite croissante et majorée converge bien mais ta suite est majorée par 10 et pourtant elle ne converge pas vers 10, par contre elle va bien converger vers le plus petit des majorants et c'est lui qu'il faut trouver.

[Lechero]

10 ? Pourquoi 10 ?

[Mortelune]

"J'ai préalablement démonter que 1 < Vn < 2"

Et parce que 10 majore bien 2, j'ai choisi 10 sans raison particulière, j'aurai pu dire Pi ou 999 ça ne changeait rien à la réflexion ;)

[Lechero]

Je suis désolé, mais je ne comprends pas...

10 > 2, c'est vrai. Mais donc en gros il faudrait dire que la suite converge vers 2 ?

[ffpower]

Justement, ce qu'était en train de te dire Benekire, c'est que c'est pas parce qu elle est majorée par 2 qu'elle converge forcément vers 2

[Lechero]

Alors comment savoir vers quelle nombre elle converge ?

[Mortelune]

Oui, suite croissante et majorée donc convergente. Après tu notes l la limite, et tu fais tendre n vers l'infini dans la relation

Avec cette idée là

[Lechero]

J'ai trouvé que la limite était + infini... Mais ça ne m'aide pas =)

[Mortelune]

Oui d'autant plus que c'est faux, fais voir ce que tu as fait qu'on puisse t'aider à trouver ton erreur ;)

[Lechero]

lim Vn+1 = lim racine(x+1)

lim x+1 = +infini
lim racine(X) = +infini

donc par le th des limites de fonctions composées, lim racine(x+1) = +infin

enfin, lim Vn+1 = lim racine(x+1) = +infini

Voilà ce que j'ai fais...

[Mortelune]

Ah oui donc ton calcul est bon partout sauf à la première ligne puisque ton égalité sans les limite est fausse. ffpower a voulu dire que comme on sait que la suite converge (croissante par la récurrence et majorée comme tu nous a dit que tu l'avais démontré au début) on peut poser l sa limite alors