Calcule d'une somme
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 25 Oct 2010, 19:46
par jack01 » 25 Oct 2010, 19:46
bonjour;
je veux quelqu'un qui peux me calculer cette somme :we:
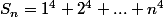
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 25 Oct 2010, 20:06
par windows7 » 25 Oct 2010, 20:06
n*(n+1)*(2n+1)*(3n²+3n-1)*(1/30)
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 27 Oct 2010, 16:25
par jack01 » 27 Oct 2010, 16:25
demonstration SVP!!
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 27 Oct 2010, 17:51
par windows7 » 27 Oct 2010, 17:51
reccurence !!!
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 27 Oct 2010, 18:01
par benekire2 » 27 Oct 2010, 18:01
Evidemment la récurrence ca marche que quand on a la formule toute belle toute gentille ...
Cherche plutôt les polynômes vérifiants P(X+1)-P(X)=X^4
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 28 Oct 2010, 11:11
par benekire2 » 28 Oct 2010, 11:11
Tu peut sinon développer (n+1)^4 et tu vera apparître n^4+.....+.... avec les "...." en fonction de n^3 n² et n , et en sommant tout le bazar tu aura une expression de la somme des puissances 4ièmes en fonction de la somme des cubes, carrés .. .

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Oct 2010, 11:16
par Ben314 » 28 Oct 2010, 11:16
Salut,
Demandant un peu plus de connaissance (binôme de Newton) mais assez simple :
Pour tout

et
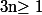
, on pose
=\sum_{k=1}^n k^e=1^e+2^e+3^e+\cdots+n^e)
.
Or, pout tout

et

on a :
^{e+1}=\sum_{p=0}^{e+1}{e+1\choose p} k^p\ \)
En sommant de
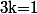
à
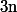
il vient :
-1^{e+1}=\sum_{p=0}^{e+1}{e+1\choose p}S_p(n))
donc
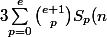=S_{e+1}(n+1)-S_{e+1}(n)-1=(n+1)^{e+1}-1)
Pour
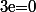
, cela signifie que
=\sum_{p=0}^0{0+1\choose p}S_p(n)=(n+1)^{0+1}-1=n\ \ \)
et, pour

, on a
+\sum_{p=0}^{e-1}{e+1\choose p}S_p(n)=(n+1)^{e+1}-1)
donc
=\frac{1}{e+1}\left( (n+1)^{e+1}-1-\sum_{p=0}^{e-1}{e+1\choose p}S_p(n)\right))
.
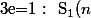 <br /> = \frac{1}{2}\left( (n+1)^2-1-{2\choose 0}S_0(n)\right)<br /> = \frac{1}{2}\left( n^2+2n-n\right) =\frac{n(n+1)}{2})
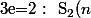 <br /> = \frac{1}{3}\left( (n+1)^3-1-{3\choose 0}S_0(n)-{3\choose 1}S_1(n)\right)<br /> = \frac{1}{3}\left( (n+1)^3-1-n-\frac{3}{2}n(n+1)\right)<br /> = \frac{n+1}{6}\left( 2(n+1)^2-2-3n\right)=\frac{n(n+1)(2n+1)}{6})
etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 28 Oct 2010, 11:53
par benekire2 » 28 Oct 2010, 11:53
J'ai lu dans tes pensées ben ... alors je t'ai devancer , mais en moins complet je te l'accorde :ptdr:
Ca me rappelle le post de Dinno ... :zen:
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 29 Oct 2010, 17:24
par jack01 » 29 Oct 2010, 17:24
oh merci ben314 et vous encore
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
