Calcule de l'infini

[Euler07]

Que donne

[Le_chat]

En fait, on utilise beaucoup la notation de sommation pour réduire la taille des "grosses sommations". Dans cette somme, on a un indice qui varie. Le plus couramment, cet indice prend des valeurs entières.



Un petit exemple:
Si je veux écrire 1/4+1/5+1/6+1/7+1/8+1/9, je vais plutot écrire.

Ici, le "n=4" signifie que:
- ton indice de sommation sera noté "n"
- la première valeur prise par n sera 4.
Le 9 au dessus de la somme signifie que la dernière valeur prise par n sera 9. Il prend donc toutes les valeurs entre 4 et 9.


Le terme général de ta somme (le 1/n) qui se situe à droite du va te dire ce que tu vas ajouter. Ici ce sont tous les 1/n, comme ton n sera entre 4 et 9, on retrouve bien 1/4+1/5+1/6+1/7+1/8+1/9.

Toi ta question, si je la transcris avec les , ce serait : si on se donne une suite de nombres , comment faire pour calculer ( remarque que l'indice de sommation est ici k et plus n!) lorsque ton n devient très grand.


Déjà, il faut s'assurer que ce que l'on écrit ne devient pas trop grand, c'est à dire que ça ne devienne pas infini si n est grand. Par exemple, si je te donne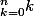 (=0+1+2+3+...+n) et bah tu peux te rendre compte que si n est grand, ton truc deviendra très grand, et quand n sera 'infini', ta somme aussi.


Par contre, si on trouve que la somme tend vers une limite bien fixée (appelons la L!) lorsque n tend vers l'infini, on écrit: . Si j'ai bien pigé la question, tu voudrais savoir de quelle manière trouver ce L.

Malheureusement, dans la plupart des cas, on ne peut pas exprimer simplement cette limite L...

Mais il ya des cas dans lesquels on peut parfaitement trouver L... regarde l'exemple de Olympus!

J'espère que tu as un peu compris mon charabia!

[nee-san]

merci de ton explication clair
donc la limite en +l'infini de 1/2+1/4+1/8.... est 2 ou non?
donc c'est pour cela que ca vaut 2?

[nee-san]

et le développement de Olympus servait à quoi

[Olympus]

et le développement de Olympus servait à quoi

Ben, peux-tu proposer une généralisation pour ?

[nee-san]

Ben, peux-tu proposer une généralisation pour ?

e quoi il faut que a partir de la je donne la forme factoriser ou que je parte de la première égalité

[beagle]

merci de ton explication clair
donc la limite en +l'infini de 1/2+1/4+1/8.... est 2 ou non?
donc c'est pour cela que ca vaut 2?

Non,ça vaut 1,
c'est avec ton 1+ la série des moitiés de moitié que tu as fait du 2.

[Dinozzo13]

Salut !

on peut utiliser des crayons de couleur
et faire du remplissage

Par analogie, on peut déterminer si un ensemble de nombre possède plus de nombre que d'autre.
Ex :
- Soit E l'ensemble des entiers pair positifs de
- est l'ensemble des entiers pairs et impairs positifs.
Lequel des deux ensembles a le plus d'éléments ?

[nee-san]

Non,ça vaut 1,
c'est avec ton 1+ la série des moitiés de moitié que tu as fait du 2.

:hum: j'ai pas trop compris ce que tu viens de me dire, ba la limite a servis a quoi

[Dinozzo13]

Est-ce que :


Autrement dit, est-ce qu'une série est une limite et réciproquement, une limite est une série ?

[beagle]

if you speak english,

"1/2 + 1/4 + 1/8 + 1/16 ... is an infinite geometric series where the first term is 1/2 and the common ratio that is multiplied by to go from term to term is also 1/2.

The formula for the sum of an infinite geometric series is S = a/(1 - r), where a is the first term and r is the common ratio.

. . . . 1/2
S = ---------- = (1/2)/(1/2) = 1 <==ANSWER"

[nee-san]

la question est posée a qui

[Ben314]

Salut,
Sinon, pour rester très très terre à terre, fait un dessin d'un rond représentant un gâteau.
Tu commence par manger 1/2 gâteau (il en reste combien ?)
Tu mange ensuite 1/4 de gâteau (il en reste combien ?)
Tu mange ensuite 1/8 de gâteau (il en reste combien ?)
Etc etc...

[beagle]

do you prefer that one:
"""Let S be the sum

"S = 1/2 + 1/4 + 1/8 + 1/16 + ...

Multiply by 2

2S = 2(1/2 + 1/4 + 1/8 + 1/16 + ...)

2S = 1 + 1/2 + 1/4 + 1/8 + 1/16 + ...

2S = 1 + S

S = 1""""

It's on internet pompage.

[beagle]

Salut,
Sinon, pour rester très très terre à terre, fait un dessin d'un rond représentant un gâteau.
Tu commence par manger 1/2 gâteau (il en reste combien ?)
Tu mange ensuite 1/4 de gâteau (il en reste combien ?)
Tu mange ensuite 1/8 de gâteau (il en reste combien ?)
Etc etc...

yes ben, that what i say,
take a maternelle child to draw this:
http://en.wikipedia.org/wiki/1/2_%2B_1/4_%2B_1/8_%2B_1/16_%2B_%C2%B7_%C2%B7_%C2%B7

[nee-san]

beagle donc cette sommes vaut 1 alor pourquoi on me dit que ca fait2
ben ba a la fin le gateau il y reste rien les part diminue et tend vers 0

[beagle]

beagle donc cette sommes vaut 1 alor pourquoi on me dit que ca fait2
ben ba a la fin le gateau il y reste rien les part diminue et tend vers 0

parce que tu as commencé à demander 1+ la série des moitiés
donc 1+1 fait 2.

si tu fais la somme des moitiés de réponses obtenues sur ce fil,
tu dois retomber sur LA réponse .

[Ben314]

beagle donc cette sommes vaut 1 alor pourquoi on me dit que ca fait2
ben ba a la fin le gateau il y reste rien les part diminue et tend vers 0

C'est parce que, dans le cas du gateau, on a fait 1/2+1/4+1/8+...
Alors que ta question de départ concernait 1+1/2+1/4+1/8+... qui, évidement, vaut 1 de plus.

[nee-san]

parce que tu as commencé à demander 1+ la série des moitiés
donc 1+1 fait 2.

si tu fais la somme des moitiés de réponses obtenues sur ce fil,
tu dois retomber sur LA réponse .

ah ok j'ai compris, donc est ce que il existe une méthode applicable pour calculer les sommes infini(je pense non), tu sais ou voulait en venir OLympus avec son développement et la généralisation qu'il ma demander

[Dinozzo13]

Salut !



Par analogie, on peut déterminer si un ensemble de nombre possède plus de nombre que d'autre.
Ex :
- Soit E l'ensemble des entiers pair positifs de
- est l'ensemble des entiers pairs et impairs positifs.
Lequel des deux ensembles a le plus d'éléments ?

Est-ce que :


Autrement dit, est-ce qu'une série est une limite et réciproquement, une limite est une série ?

@Nee-san : A ceux qui s'y intéresse :++: