Calcule de l'infini
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 17:45
par nee-san » 15 Déc 2010, 17:45
bonjour a tous, alors j'aurait une question à posé: Comment les mathématiciens calcule til de grande sommes voire des sommes infini? :mur:
merci a ceux qui me répondrons
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 17:47
par Euler07 » 15 Déc 2010, 17:47
Tu peux être précis(e) ? Les ordinateurs sinon
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 17:49
par nee-san » 15 Déc 2010, 17:49
Euler07 a écrit:Tu peux être précis(e) ? Les ordinateurs sinon
ba une somme du type 1+1/2+1/4+1/8..... par exemple
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 17:50
par Euler07 » 15 Déc 2010, 17:50
C'est avec des formules bien précises que l'on fait cela... T'en connais pas ?
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 17:51
par nee-san » 15 Déc 2010, 17:51
Euler07 a écrit:C'est avec des formules bien précises que l'on fait cela... T'en connais pas ?
non pas du tout
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 17:54
par Euler07 » 15 Déc 2010, 17:54
Ah je suppose donc que tu es en 2nd
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 17:56
par nee-san » 15 Déc 2010, 17:56
Euler07 a écrit:Ah je suppose donc que tu es en 2nd
oui tu as raisons

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Déc 2010, 17:59
par Olympus » 15 Déc 2010, 17:59
Salut !
Pour les sommes infinies, on les appelle "séries" .
Pour ton exemple :
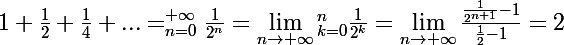
.
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 18:02
par Euler07 » 15 Déc 2010, 18:02
Vas t il comprendre facilement ??
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 18:03
par nee-san » 15 Déc 2010, 18:03
j'ai paratiquement rien compris mais d'ou sort le
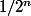
et le
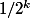
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 18:05
par Euler07 » 15 Déc 2010, 18:05
n varie si tu veux... En n=0 tu as 1 ect..
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 15 Déc 2010, 18:06
par beagle » 15 Déc 2010, 18:06
Pour cette série des moitiés on peut utiliser des crayons de couleur
et faire du remplissage,
c'est pas très mathématique,
mais on peut se faire aider d'un gamin de maternelle,...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 18:08
par nee-san » 15 Déc 2010, 18:08
en faite je comprend pas comment a partir de la première forme on arrive a des sommes avec
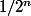

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Déc 2010, 18:10
par Olympus » 15 Déc 2010, 18:10
Développe
\left(x^2+xy+y^2\right))
, puis
\left(x^3+x^2y+xy^2+y^3\right))
. Peux-tu généraliser ?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 18:11
par Euler07 » 15 Déc 2010, 18:11
Regarde 1+2+3+........+n donne par exemple \bigsum_{k=1}^{n} \{k}
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 18:15
par nee-san » 15 Déc 2010, 18:15
Olympus a écrit:Développe
\left(x^2+xy+y^2\right))
, puis
\left(x^3+x^2y+xy^2+y^3\right))
. Peux-tu généraliser ?
alors le développement je trouve
1)x²y+y²x-xy-y²
2)

c'est ca

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Déc 2010, 18:28
par Olympus » 15 Déc 2010, 18:28
Oups, ce sont des "y" à la place de mes "1", je viens d'éditer .
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 18:32
par nee-san » 15 Déc 2010, 18:32
je trouve alors:
1)

2)

-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 15 Déc 2010, 18:34
par Euler07 » 15 Déc 2010, 18:34
T'es sur pour la 1 ?
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 15 Déc 2010, 18:36
par nee-san » 15 Déc 2010, 18:36
Euler07 a écrit:T'es sur pour la 1 ?
ah non j'obtient
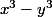
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
