Continuité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
azerty123456
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Oct 2010, 11:48
-
par azerty123456 » 26 Oct 2010, 12:15
bonjour besoin d'aide pour ce devoirs maison
1)calculer f(2) cette fonction est elle continue en 2 =>je pense qu'il faut calculer la limite a doite et a gauche mais je ne sais pas comment m'y prendre
4) démontrer que pour tout
,
=(x-2n)^2(2n+2-x))
informations Soit f la fonction définie sur R par
si x appartient [0;2[
=x^2(2-x))
et pour tout réel x,
=f(x))
=merci pour votre aide
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 26 Oct 2010, 12:21
Bonjour,
Une fonction
est continue en
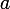
si, et seulement si,
=\lim_{x\to a^+}f(x)=f(a))
.
Tu sais calculer une limite ? Cest pareil pour la limite à droite et à gauche.
-
azerty123456
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Oct 2010, 11:48
-
par azerty123456 » 26 Oct 2010, 12:24
oui, je trouve que la fonction est continue en 2 c'est bien sa ?
pour la question 4 je ne sais vraiment pas ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 26 Oct 2010, 12:27
Comment as-tu fait pour calculer
)
?
-
azerty123456
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Oct 2010, 11:48
-
par azerty123456 » 26 Oct 2010, 17:58
je trouve que f(2)=f(0)=0
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 26 Oct 2010, 18:07
Mais je ne comprends pas car ta fonction est défini sur
donc tu ne devrais pas pouvoir calculer
...
Il ny aurait pas une autre expression de
si
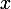
a dautres valeurs ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 26 Oct 2010, 19:25
Salut,
sa fonction est définie sur R, elle vaut ce qui est écrit sur [0;2[ puis on complète sur R par 2-périodicité.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 26 Oct 2010, 19:33
Nightmare a écrit:Salut,
sa fonction est définie sur R, elle vaut ce qui est écrit sur [0;2[ puis on complète sur R par 2-périodicité.
Merci.
Donc
=f(4))
ou je nai rien compris ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 26 Oct 2010, 19:36
Ben oui, mais tout ceci était écrit dans l'énoncé :
et pour tout réel x,
=f(x))
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 26 Oct 2010, 19:47
Nightmare a écrit:Ben oui, mais tout ceci était écrit dans l'énoncé :
OK, merci.
Mais du coup
=f(4)=4^2(2-4)=-32)
et non
?
-
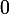
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 27 Oct 2010, 00:18
Pourquoi f(4)=4²(2-4) ? f(x)=x²(2-x) seulement sur [0;2[ !
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 27 Oct 2010, 00:51
Nightmare a écrit:Pourquoi f(4)=4²(2-4) ? f(x)=x²(2-x) seulement sur [0;2[ !
Mais comment faire pour calculer la valeur de
dans ce cas ? :hein:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 27 Oct 2010, 00:58
f(2)=f(0+2)=f(0) !
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 27 Oct 2010, 01:06
Nightmare a écrit:f(2)=f(0+2)=f(0) !
Merci.
Bonne nuit.
-
azerty123456
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Oct 2010, 11:48
-
par azerty123456 » 28 Oct 2010, 09:42
donc j'ai raison en disant que en 2 la fonction est continue ou pas?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
par Jimm15 » 28 Oct 2010, 10:39
azerty123456 a écrit:donc j'ai raison en disant que en 2 la fonction est continue ou pas?
Daprès ce que jai compris :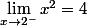
et
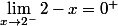
Donc
=0^+)
.
=f(0))
donc
=\lim_{x\to0^+}f(x))
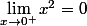
et
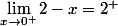
Donc
=0^+)
.
Conclusion : =\lim_{x\to2^+}f(x)=0^+)
donc est continue en 
.
-
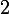azerty123456
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Oct 2010, 11:48
-
par azerty123456 » 28 Oct 2010, 12:04
oui, c'est a peu près ce que j'ai fait par contre pour la question 4 on m'a conseillé d'utiliser "la récurence" mais je ne vois pas ce que s'est ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
