Prolongement par continuité

[Hardtoexplain91]

Bonsoir, comment montrer qu'une fonction peut se prolonger par continuité en 0 et 2pi ?

je veux juste savoir la méthode,

merci

[uztop]

Bonsoir,

une fonction se prolonge par continuité en 0 par exemple si elle admet une limite quand f tend vers 0. Cela suppose bien entendu que 0 n'est pas dans l'ensemble de définition (sinon, il n'y a pas de prolongement à faire)

[Hardtoexplain91]

bonsoir uztop, finalement j'ai un problème de maths qui me pose problème.. pourrais-tu m'aider à en comprendre la correction?..

je le poste tout de suite :)

[uztop]

oui, tu peux poser ta question :)

[Hardtoexplain91]

J'ai quelque soit x appartenant à ]0,2[, f(x)= ()cotan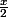 , je dois montrer qu'elle se prolonge par continuité en ]0,2[, tout en calculant f(0) et f(2). Le problème est que je trouve 0 pour les deux.. ce qui ne peut être possible, car je dois ensuite comparer f(2-x) et f(x) pour en déduire la représentation graphique (en faîte on trouve un centre de symétrie..)

[uztop]

oui, on trouve effectivement 0 pour les deux, mais je ne vois pas en quoi c'est un problème.
Tu as calculé ? Tu trouves quoi ?

[Hardtoexplain91]

je bloque pour le prolongement en faîte..

[uztop]

la limite vaut 0; elle est donc bien définie.
f peut donc se prolonger par continuité en 0 et en 2 Pi avec f(0) = 0 et

[Hardtoexplain91]

dans la correction, on dit que f(0) = -1 et que f(2pi ) = 1, ensuite ils calculent f(x) avec x = 2pi- h , jcomprends pas.. :doh:

[uztop]

j'ai refait les calculs et ... le corrigé est juste
En fait, pour le montrer, tan(x) est équivalent à x en 0 (est ce que tu as vu les équivalents) ?
Pour le 2pi -h, c'est pour montrer que f(2pi-h)=-f(h); on peut l'appeler h ou x, ça ne change pas grand chose.

[Hardtoexplain91]

Jcomprends rien ... :triste:

Vous pourriez pas me corriger cet exercice, j'ai la correction sous les yeux, mais j'arrive pas à comprendre..

Je vous mets l'énoncé :

Soit la fonction f définie par quelque soit x appartenant à ]0,2[, f(x)=.

a) Montrer que f se prolonge par continuité en 0 et 2.

b) calculer f(0) et f(2), (je suppose qu'il faut calculer la limite puisqu'on a des formes indéterminées .. mais jcomprends pas..)

c) Comparer f(2-x) et f(x). Que peut-on en éduire pour la représentation graphique.