Analyse

[magnum]

Bonjour,
je n'aime pas trop ce genre d'exo, car on ne sait jamais par où commencer..toute aide est la bienvenue

Trouver toutes les fonctions f de R+ vers R pour lesquelles il existe k>0 et a > 1 verifiant :
Pour tout (x,y) positifs,
A-t-on Ie meme resultat avec 0 < a < 1?

Merci !

[girdav]

Bonsoir,
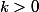
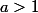
on peut réécrire l'hypothèse comme étant il existe et tel que pour tous , .

[magnum]

ah oui, ça m'aide beaucoup merci !

mais à quoi sert l'hypothèse, x,y positifs ?

je trouve que f est constante sur R+ et que le résultat reste valide pour a dans ]0,1[.

[girdav]

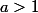
D'accord pour le cas où . Pour le second, pense à des fonctions de la forme .

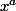
[magnum]

Mais comment sait-on que x^a est solution ?(j'ai réussi à la vérifier pour racine par ex. mais dans le cas où a est dans 0,1 je ne vois pas de méthode générale pour le vérifier.
Sinon, comment être sûr qu'il n'y a pas d'autres fonctions possibles ?

[girdav]

Attention, je ne dis pas que pour .
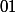
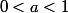
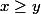
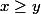
Pour montrer que pour on a , on peut se restreindre au cas . Pour fixé, on pose et on montre que cette fonction est négative pour tout . Une étude de fonctions doit en venir à bout.