Problème lors du calcul d'une intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 11 Juil 2010, 12:50
par balteo » 11 Juil 2010, 12:50
Bonjour,
Je souhaite intégrer la fonction suivante:
int(1/(1+exp(-x)), x) (1)
J'ai tenté par substitution comme ceci:
Je pose u = 1+exp(-x)
Je sais que du = exp(-x) * dx donc dx = du * exp(x)
expression (1) = int( 1/u * exp(x) * du)
Je trouve ensuite:
expression (1) = ln(u) * exp(x) + C = ln(1+exp(-x)) * exp(x) + C
Or un logiciel de calcul formel me donne:
ln(1+exp(-x)) - ln(exp(-x))
Où ai-je commis une erreur?
Merci d'avance pour vos réponses,
J.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Juil 2010, 16:41
par Sa Majesté » 11 Juil 2010, 16:41
Ici
balteo a écrit:Je pose u = 1+exp(-x)
Je sais que du = exp(-x) * dx
du = -exp(-x) dx = (1-u) dx
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 11 Juil 2010, 17:04
par ft73 » 11 Juil 2010, 17:04
enfin bon, cette intégrale est tombée au bac S en 2003.
Ici, une petite multiplication par exp(x) en haut et en bas suffit ?
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 11 Juil 2010, 17:28
par balteo » 11 Juil 2010, 17:28
ft73 a écrit:enfin bon, cette intégrale est tombée au bac S en 2003.
Ici, une petite multiplication par exp(x) en haut et en bas suffit ?
Merci! Mais comment je procède pour trouver la primitive après avoir multiplié par exp(x) en haut et en bas?
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 11 Juil 2010, 17:30
par balteo » 11 Juil 2010, 17:30
Sa Majesté a écrit:Ici
du = -exp(-x) dx = (1-u) dx
Effectivement. Merci! Cela dit je bloque toujours au même point après...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Juil 2010, 18:17
par Sa Majesté » 11 Juil 2010, 18:17
balteo a écrit:Effectivement. Merci! Cela dit je bloque toujours au même point après...
Ben c'est toi qui proposes cette méthode alors je pensais que c'était OK
} = \int \left(\frac{1}{u}+\frac{1}{1-u}\right) du = \ln|u| - \ln|1-u| + C = \ln \frac{1+e^{-x}}{e^{-x}} + C = \ln \left(e^x + 1\right) + C)
Sinon
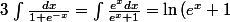 + C)
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 12 Juil 2010, 10:09
par balteo » 12 Juil 2010, 10:09
Sa Majesté a écrit:Ben c'est toi qui proposes cette méthode alors je pensais que c'était OK
} = \int \left(\frac{1}{u}+\frac{1}{1-u}\right) du = \ln|u| - \ln|1-u| + C = \ln \frac{1+e^{-x}}{e^{-x}} + C = \ln \left(e^x + 1\right) + C)
Sinon
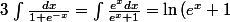 + C)
Merci. J'y suis presque! Par contre, je viens de chercher dans mes ouvrages pour trouver comment intégrer
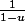
et je ne trouve pas la réponse.
Je sais que la réponse est -log(1-u). Quelqu'un peut-il me dire d'après quelle règle on trouve cela svp?
Merci,
J.
-
mathelot
 par mathelot » 12 Juil 2010, 11:36
par mathelot » 12 Juil 2010, 11:36
balteo a écrit:Merci. J'y suis presque! Par contre, je viens de chercher dans mes ouvrages pour trouver comment intégrer
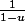
et je ne trouve pas la réponse.
Je sais que la réponse est -log(1-u). Quelqu'un peut-il me dire d'après quelle règle on trouve cela svp?
Merci,
J.
dérivée de fonction composée
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 12 Juil 2010, 16:37
par balteo » 12 Juil 2010, 16:37
Merci à vous! J'ai pigé maintenant.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
