Bonjour à tous,
J'ai un ami qui va tenter l'examen d'entrée à l'école des officiers mais comme ça fait 4ans qu'on a plus fait de math, on a du mal avec certaines questions.
Est-ce que vous pouvez nous aider?
Même une réponse à une question, ça ferait plaisir:
1) Pour quelle valeur de a (appartient à R) le système suivant (inconnues x et y) a-t-il a)1solution b)une infinité de solution c) pas de solution
2x+ay=5
x-y=a
2)Recherchez l'équation de l'asymptote oblique y=ax+b de la fonction f où
a = lim f(x)/x b=lim (f(x)-ax) f(x)=(3x²+2x+1)/2x
3) Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
4) sachant que le log(10)2=a avec a appartenant à R, calculez log(10) (racine8) /32 en fonction de a
5) si cotg=2 et sin(x)<0, calculer cos(x)
J'en ai encore quelque une mais cela on est vraiment perdu.
Merci
Test pour rentrée à l'armée : log, asymptote, trigo
11 messages
- Page 1 sur 1
par Arnaud-29-31 » 21 Juin 2010, 21:50
Bonjour,
Pour le 1), chaque équation représente une droite. Les solutions du système sont les points (x,y) situés sur les deux droites. Donc si les deux droites sont
- confondues : infinité de solution
- parallèles : pas de solutions
- sécantes : une solution
Pour le 2), on sait que y = ax+b est asymptote oblique ssi f(x) - (ax+b) tend vers 0 en +l'infini.
Il faut donc transformer l'écriture de f(x) pour exhiber a et b en écrivant f(x) = ax + b + "qqch qui tend vers 0"
3) Un peu plus dur, un schéma peut aider, il s'agit du cercle de centre (2,0) et de rayon 1. On cherche les deux droites passant par l'origine et tangente au cercle.
C'est deux droites sont de la forme y = ax, on réinjecte y = ax dans l'équation du cercle : ceci nous donne un trinôme d'inconnue x. Or on sait qu'il n'y a qu'une x possible, le discriminant du trinôme est donc nul ce qui nous donne a.
4) Il faut exprimer sqrt(8)/32 comme produit de puissances de 2 et utiliser les propriété du log.
5) cotan = cos/sin ... cotan(x) est positif donc si sin(x) négatif, cos(x) doit l'être aussi quel est l'angle dont le cosinus et le sinus sont négatifs et tel que son cosinus vaut 2 fois son sinus ? (Toujours faire un ptit schéma du cercle trigo)
Pour le 1), chaque équation représente une droite. Les solutions du système sont les points (x,y) situés sur les deux droites. Donc si les deux droites sont
- confondues : infinité de solution
- parallèles : pas de solutions
- sécantes : une solution
Pour le 2), on sait que y = ax+b est asymptote oblique ssi f(x) - (ax+b) tend vers 0 en +l'infini.
Il faut donc transformer l'écriture de f(x) pour exhiber a et b en écrivant f(x) = ax + b + "qqch qui tend vers 0"
3) Un peu plus dur, un schéma peut aider, il s'agit du cercle de centre (2,0) et de rayon 1. On cherche les deux droites passant par l'origine et tangente au cercle.
C'est deux droites sont de la forme y = ax, on réinjecte y = ax dans l'équation du cercle : ceci nous donne un trinôme d'inconnue x. Or on sait qu'il n'y a qu'une x possible, le discriminant du trinôme est donc nul ce qui nous donne a.
4) Il faut exprimer sqrt(8)/32 comme produit de puissances de 2 et utiliser les propriété du log.
5) cotan = cos/sin ... cotan(x) est positif donc si sin(x) négatif, cos(x) doit l'être aussi quel est l'angle dont le cosinus et le sinus sont négatifs et tel que son cosinus vaut 2 fois son sinus ? (Toujours faire un ptit schéma du cercle trigo)
par lrt88 » 22 Juin 2010, 06:39
Merci de ton aide.
On va se pencher là-dessus et on va essayer de comprendre.
On va se pencher là-dessus et on va essayer de comprendre.
par busard_des_roseaux » 22 Juin 2010, 07:45
Bj,
Quelque soit le pays, le métier est devenu difficile
avec toutes ces guerres :lol2:
on multiplie la 2ème égalité, membre à membre, par a
on additionne
x=5+a^2)
on multiplie la 2ème égalité par 2
(a+2)y=5-2a
d'où la discussion
si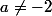
une solution unique
si
0y=9 pas de solution.
={3 \over 2}x +1 +1/2x={3 \over 2}x +1 +o(1))
la courbe de f admet pour asymptote oblique
la droite d'équation
et le signe de 1/x donne la position de la courbe par rapport
à la droite asymptote
la tangente est positive et le sinus < 0. il s'agit d'un point du cercle
trigonométrique dans le 3ème quadrant x<0 et y<0
utiliser={1 - cos^2(x) \over cos^2(x)})
pour calculer)
cos(x)<0
lrt88 a écrit:J'ai un ami qui va tenter l'examen d'entrée à l'école des officiers
Quelque soit le pays, le métier est devenu difficile
avec toutes ces guerres :lol2:
lrt88 a écrit:1) Pour quelle valeur de a (appartient à R) le système suivant (inconnues x et y) a-t-il a)1solution b)une infinité de solution c) pas de solution
2x+ay=5
x-y=a
on multiplie la 2ème égalité, membre à membre, par a
on additionne
on multiplie la 2ème égalité par 2
(a+2)y=5-2a
d'où la discussion
si
une solution unique
si
0y=9 pas de solution.
la courbe de f admet pour asymptote oblique
la droite d'équation
et le signe de 1/x donne la position de la courbe par rapport
à la droite asymptote
la tangente est positive et le sinus < 0. il s'agit d'un point du cercle
trigonométrique dans le 3ème quadrant x<0 et y<0
utiliser
pour calculer
cos(x)<0
par busard_des_roseaux » 22 Juin 2010, 08:32
lrt88 a écrit:Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
Soit (a,b) les coordonnées du point de tangence
passe par l'origine
d'où une équation du second degré d'inconnue
par lrt88 » 23 Juin 2010, 20:46
Merci pour ses réponses mais je dois avouer qu'on est encore perdu !
1) Pour quelle valeur de a (appartient à R) le système suivant (inconnues x et y) a-t-il a)1solution b)une infinité de solution c) pas de solution
2x+ay=5
x-y=a
=> on a compris le développement de busard_des_roseaux mais pas les conclusions. Pourquoi peut-on dire qu'il ya qu'une solution, une infinité de solution et pas de solution ?
Parce que cette question n'est qu'un exemple qu'il aura au test donc on aimerait connaitre la théorie en quelques sortes.
2) Recherchez l'équation de l'asymptote oblique y=ax+b de la fonction f où
a = lim f(x)/x b=lim (f(x)-ax) f(x)=(3x²+2x+1)/2x
On a essayé d'appliqué la théorie mais pour le calcul de "a" on obtient infini/infini. Donc selon notre résultat, alors on a utilisé le truc de l'hospital (on a fait les dérivés) et au final on a eu a=2 et b=-2. Est-ce que ca parait juste? busard_des_roseaux arrivait a une autre conclu mais on sait comment il a fait !
3) Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
Comment est-ce que vous savez qu'il s'agit d'un cercle de centre (2,0) ?
4) sachant que le log(10)2=a avec a appartenant à R, calculez log(10) (racine8) /32 en fonction de a
On n'a réussi :D
5) si cotg=2 et sin(x)<0, calculer cos(x). On s'est rendu compte en demandant à d'autre de notre classe que à l'époque, la prof avait presque tout sauté la trigo. Est-ce que vous connaissez pas un bon lien pour nous apprendre ce fameux cercle trigo?
1) Pour quelle valeur de a (appartient à R) le système suivant (inconnues x et y) a-t-il a)1solution b)une infinité de solution c) pas de solution
2x+ay=5
x-y=a
=> on a compris le développement de busard_des_roseaux mais pas les conclusions. Pourquoi peut-on dire qu'il ya qu'une solution, une infinité de solution et pas de solution ?
Parce que cette question n'est qu'un exemple qu'il aura au test donc on aimerait connaitre la théorie en quelques sortes.
2) Recherchez l'équation de l'asymptote oblique y=ax+b de la fonction f où
a = lim f(x)/x b=lim (f(x)-ax) f(x)=(3x²+2x+1)/2x
On a essayé d'appliqué la théorie mais pour le calcul de "a" on obtient infini/infini. Donc selon notre résultat, alors on a utilisé le truc de l'hospital (on a fait les dérivés) et au final on a eu a=2 et b=-2. Est-ce que ca parait juste? busard_des_roseaux arrivait a une autre conclu mais on sait comment il a fait !
3) Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
Comment est-ce que vous savez qu'il s'agit d'un cercle de centre (2,0) ?
4) sachant que le log(10)2=a avec a appartenant à R, calculez log(10) (racine8) /32 en fonction de a
On n'a réussi :D
5) si cotg=2 et sin(x)<0, calculer cos(x). On s'est rendu compte en demandant à d'autre de notre classe que à l'époque, la prof avait presque tout sauté la trigo. Est-ce que vous connaissez pas un bon lien pour nous apprendre ce fameux cercle trigo?
par busard_des_roseaux » 23 Juin 2010, 21:11
aloha,
La théorie est toute simple !
grosso modo, les seuls systèmes que l'on sache résoudre
sont de dimensions nxn
autant d'inconnues que d'équations
le système s'écrit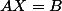
et admet une solution si B est combinaison linéaire
des vecteurs colonnes de la matrice A
si il y a trop d'inconnues (n) et pas suffisamment d'équations (p)
on "passe" n-p inconnues à droite qui servent de paramètres
si il y a trop d'équations (p)
on calcule les inconnues, puis il y a p-n contraintes supplémentaires
à vérifier.
on divise chaque terme de la somme par x.
(x-2)²+y² est la distance d'un point M(x;y) à U(2;0)
5) si cotg=2 et sin(x)<0, calculer cos(x). On s'est rendu compte en demandant à d'autres de notre classe que à l'époque, la prof avait presque tout sauté la trigo. Est-ce que vous connaissez pas un bon lien pour nous apprendre ce fameux cercle trigo?
google est ton ami: chercher wiki+cercle+trigo
les idées de la trigonométrie:
1) les arcs de cercles ont une longueur: on les mesure en
les approchant par des lignes polygonales inscrites et exinscrites
2) les longueurs d'arc servent à mesurer les angles au centre:
au lieu de prendre comme mesure d'angle le mètre, ce qui ferait
dépendre du cercle choisi, on mesure les angles donc les arcs en
radians (radius=rayon)
3) les angles de vecteurs (de longueur 1) sont des rotations:
quand on compose ces rotations, on note cette opération par
un signe + : on obtient le groupe des angles.
4) il y a une application surjective des nombres réels (la droite réelle)
sur le groupe des rotations: chaque nombre appartient
à la classe , modulo
, de la mesure d'angle d'une rotation.
lrt88 a écrit:Parce que cette question n'est qu'un exemple qu'il aura au test donc on aimerait connaitre la théorie en quelque sorte.
La théorie est toute simple !
grosso modo, les seuls systèmes que l'on sache résoudre
sont de dimensions nxn
autant d'inconnues que d'équations
le système s'écrit
et admet une solution si B est combinaison linéaire
des vecteurs colonnes de la matrice A
si il y a trop d'inconnues (n) et pas suffisamment d'équations (p)
on "passe" n-p inconnues à droite qui servent de paramètres
si il y a trop d'équations (p)
on calcule les inconnues, puis il y a p-n contraintes supplémentaires
à vérifier.
lrt88 a écrit:2) Recherchez l'équation de l'asymptote oblique y=ax+b de la fonction f où
a = lim f(x)/x b=lim (f(x)-ax) f(x)=(3x²+2x+1)/2x
on divise chaque terme de la somme par x.
lrt88 a écrit:3) Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
Comment est-ce que vous savez qu'il s'agit d'un cercle de centre (2,0) ?
(x-2)²+y² est la distance d'un point M(x;y) à U(2;0)
5) si cotg=2 et sin(x)<0, calculer cos(x). On s'est rendu compte en demandant à d'autres de notre classe que à l'époque, la prof avait presque tout sauté la trigo. Est-ce que vous connaissez pas un bon lien pour nous apprendre ce fameux cercle trigo?
google est ton ami: chercher wiki+cercle+trigo
les idées de la trigonométrie:
1) les arcs de cercles ont une longueur: on les mesure en
les approchant par des lignes polygonales inscrites et exinscrites
2) les longueurs d'arc servent à mesurer les angles au centre:
au lieu de prendre comme mesure d'angle le mètre, ce qui ferait
dépendre du cercle choisi, on mesure les angles donc les arcs en
radians (radius=rayon)
3) les angles de vecteurs (de longueur 1) sont des rotations:
quand on compose ces rotations, on note cette opération par
un signe + : on obtient le groupe des angles.
4) il y a une application surjective des nombres réels (la droite réelle)
sur le groupe des rotations: chaque nombre appartient
à la classe , modulo
par lrt88 » 24 Juin 2010, 13:42
1) Pour quelle valeur de a (appartient à R) le système suivant (inconnues x et y) a-t-il a)1solution b)une infinité de solution c) pas de solution
2x+ay=5
x-y=a
Dans quel cas d'équation, on a une infinité de solution ? car dans notre exercice ya un "a" sans solution et des "a" avec une solution unique.
3) Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
On a trouvé les caractéristiques du cercle ! On a l'équation de la droite qu'on réimplante dans l'équation du cercle mais on obtient des égalités avec a, x et y. Comment trouve-t-on une valeur pour a?
Pour la 5, selon une personne, cos(x)=2sin(X) or selon un autre avec les formules de la Tg (tg=1/cotg et 1+tg²=1/cos²), cos(x)=racine de 4/5. Qui a raison ?
Encore merci
2x+ay=5
x-y=a
Dans quel cas d'équation, on a une infinité de solution ? car dans notre exercice ya un "a" sans solution et des "a" avec une solution unique.
3) Calculer les équations passant à l'origine et tangentes au cercle d'équation (x-2)²+y²=1
On a trouvé les caractéristiques du cercle ! On a l'équation de la droite qu'on réimplante dans l'équation du cercle mais on obtient des égalités avec a, x et y. Comment trouve-t-on une valeur pour a?
Pour la 5, selon une personne, cos(x)=2sin(X) or selon un autre avec les formules de la Tg (tg=1/cotg et 1+tg²=1/cos²), cos(x)=racine de 4/5. Qui a raison ?
Encore merci
par busard_des_roseaux » 25 Juin 2010, 06:51
re-bonjour,
pour la (5)
={ 1 \over 1+tan^2(x)})
=\frac{1}{1+\frac{1}{4}}=\frac{4}{5})
= - \frac{2}{\sqrt{5}})
le cosinus est négatif car tan(x)>0 et sin(x)<0
pour la (1), le seul cas où le système n'admet pas une unique solution est
a=-2
mézalor
2(x-y)=5
x-y=-2
on voit que c'est impossible car
est égal à 5/2 et à - 2
pour la (5)
le cosinus est négatif car tan(x)>0 et sin(x)<0
pour la (1), le seul cas où le système n'admet pas une unique solution est
a=-2
mézalor
2(x-y)=5
x-y=-2
on voit que c'est impossible car
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 121 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :