Defi A Tous Les Participants

[Nota-Bene19]

Salut ;

1er EXE : :++: [SIZE=7]xxx[/SIZE]

Dans l'espace soit (P) le plan donné par son équation cartésienne:
(P): x+y-z=1 et (D) : x-2=2y-2=z-1 .

Donner l'expression anlytique de :

1° la projection sur (P) parallélement à (D).
2° la symétrie par rapport à (D) de direction (P) .

2eme EXE : :++:

Soit n un entier non nul , N² < n .

Montrer que [ racine(n+1)-racine(n) < 1/2N ]

[yos]

Pourquoi Défi?
Première question.
M(a,b,c).
D a pour représentation paramétrique (2t, t, 2t-1)
La parallèle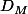 à D passant par M a pour représentation paramétrique (2t+a, t+b, 2t+c).
Elle coupe P pour 2t+a+t+b-(2t+c)=1, c'est-à-dire t=-a-b+c+1.
Le projeté M' de M a donc pour coordonnées
(-a-2b+2c+2, -a+c+1, -2a-2b+3c+2).
Modulo les erreurs de calculs.

[Pythales]

En multipliant par la quantité conjuguée :

Petit défi !

[Nota-Bene19]

Salut Phytales;Yos :

Yos : je ne sais pas si ta 1ère réponse est vraie ou non , mais ou est la 2ème ,tu l'as oubliée ? je vais te donner ma réponse mais pas mnt .

Phytales : je ne crois pas que c une bonne idée !!! t'as pas réflichi au théorème des accroissements finis ? ça sera très facile et très intelligent de l'utiliser , mais je te laisse ça à faire en choisissant l'intervalle et la fonction .

ça reste un défi pour vous !!!

A++. :+++: :+++: :+++: :wc:

[Pythales]

Pourquoi faire simple quand on peut faire compliqué ?

[Fract83]

Hello,

Pythales, "Pourquoi faire simple quand on peut faire compliqué ?"

Eh bien, par exemple lorsque ton prof te demande de faire l'exercice suivant:

Soit n un entier non nul , N² < n .
Montrer que [ racine(n+1)-racine(n) < 1/2N ] en utilisant le theoreme des accroissements finis.

Tu comprends ce que je veux dire ? :-)

Bonne journee.

PS : Je suis d'autant plus conforte dans mon idee que ce "defi" est ridicule...

[yos]

Yos : je ne sais pas si ta 1ère réponse est vraie ou non , mais ou est la 2ème ,tu l'as oubliée ? je vais te donner ma réponse mais pas mnt .

1) Si tu as la réponse, tu devrais pouvoir juger de l'exactitude de la mienne.

2) La seconde question est aussi facile que la première. Qui plus est si tu as la réponse, je ne la ferai pas.

Il s'agit de questions niveau terminale S . Tu peux donc les poser à la rubrique lycée. De plus elles sont tout à fait classiques, donc elles ne méritent pas trop l'appellation de défi que je réserverais à des exercices genre olympiades ou énigmes (voir rubriques correspondantes).

Quant à l'exercice 2, je pense, comme Pythalès, que l'usage du TAF est un marteau pour assommer une mouche.

En espérant ne pas t'avoir vexé.

[Nota-Bene19]

Hello;

Aucune personne n'a répondu complétement alors pourquoi vous dites des choses : c'est pas un défi ...etc ?.

Aucun n'a pu résolu ces deux exes tous les deux . alors ça vraiment bizarre .

c un défi parce que ces exes mérite utiliser l'intelligence .

moi ce que je cherche c avoir des amis qui font le Maths peut être comme vous :++: :++: :++:

Au revoir !!!