Etude de fonction

par **ned aero** » 28 Mar 2010, 15:18

oui erreur, j'ai inversé...à force d'inverser des inverses déjà inversés....

je n'ai pas fait le calcul....

bonne continuation

par **sokep** » 28 Mar 2010, 15:20

bonjour je suis super nulle en math ...sil vous plaittt est ce que quelqu un pourrait m`aider ..je doit remettre ce devoir demain :triste: et je ne comprend pa.....

soit f la fonction definie par f(x)=(2x^2-3x+6)/x+4
soit f la courbe representative de la fonction f
1)determiner les 3 reels a,b et c tel que : (a)/(x+4)bx+c
2)deterrminer les limites de f en fonction de +infini et -infini
3)demontrer que cf admet une asymptote oblique notee delta en +infini et -infini
4)etudier la position de la cf par rapport a son asymptote delta en +infini et en - infini
5)etudier les limites de f(x) quand x tend vers -4.. integrer graphiquement
6)dresser le tableau de variation de f

par **saralecompte** » 28 Mar 2010, 15:23

oui lol j comprend :we:
J ai simplement mis au même dénominateur et simplifier ce qu il y avait dans la parenthèse

par **saralecompte** » 28 Mar 2010, 15:25

je ne comprend ta premier question? ils sortent d où les a, b et c?
Si tu veux que plusieurs personne t aident je te conseil de remettre ton message dans un nouveau sujet ;)

par **saralecompte** » 28 Mar 2010, 15:51

saralecompte a écrit:Finalement je trouve ca:

Non finalement je me suis trompée, je trouve ca:

par **saralecompte** » 28 Mar 2010, 16:54

Le tableau de signe de ma dérivée seconde ne correspond pas à mon graphique, je trouve des concavité inverse de ce que je devrais avoir je revérifié mes calculs mais je n arrive pas à trouver ma fautes,

Voici mes résultats j ai aussi scanné le début en corrigeant mes fautes de départ,

Merci de jeter un oeil :happy2:

[CENTER]

[/CENTER]

par **munos280** » 28 Mar 2010, 17:25

bonjour , j'aurais besoin d'une petite aide .

je doit faire le domaine de defintion de sin3x . pourriez vous m'aider.
J'ai commencé mais je sais pas si c'est exact ? :we:

la fonction a pour domaine de defintion R
la fonction est impaire car f(-x)=sin3(-x) est différent -f(x)=-sin3x
la périodicité sin 3kpi la fonction est donc une periode
f'(x)=cos3x

voila merci de votre aide

par **Sa Majesté** » 28 Mar 2010, 17:33

Voici ce que je trouve pour f"

par **saralecompte** » 28 Mar 2010, 17:38

Merci, mais ca veux dire que tout ce que j ai fait est faut ceux qui m on aidez à faire ca on faut aussi?
Je ne sais pas comment tu as obtenu ca mais ca ne m aide pas c est possible de m indiquer où j ai fait ma faute ?

munos280, si tu veux avoir plus de chance pour qu on t aide je te conseil de poster ta question dans un nouveau sujet ;)

par **mathelot** » 28 Mar 2010, 18:03

Bj,

remarque
l'inverse de

est

la dérivée d'une fonction composée

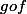est donnée par

ici

est homographique et

est la racine carrée

en simplifiant

ensuite , pour la dérivée seconde , utilise la formule de
Leibniz de dérivation d'un produit
(uv)'=u'v+uv'

factorisons une des racines, elles sont inverses l'une de l'autre

par **saralecompte** » 28 Mar 2010, 18:23

Merci beaucoup Mathelot, je comprend bien ce que tu fais tu ne sais pas me dire où j ai fait ma faute pour que j ai plus facile SVP, si je recommence tout mon calcule je retomberai sur la même chose :cry:

par **mathelot** » 28 Mar 2010, 19:08

après factorisation de la racine

<--- c bon, g demandé à ma calculatrice

tu veux que je regarde dans ton brouillon :doh:

par **mathelot** » 28 Mar 2010, 19:23

je n'ai pas regardé en détail, il y a des maladresses
dans la façon de conduire les calculs:

i)
tu ne dois pas travailler avec des quotients à 4 étages
du style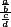

pour diviser par un quotient, multiplier par l'inverse

ii)
factoriser les dénominateurs:
quand les calculs sont lourds, préférer l'écriture

à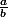

iii) quand on dérive une racine
écrire directement l'inverse de la racine au lieu de diviser

par **Sa Majesté** » 28 Mar 2010, 19:26

mathelot a écrit: <--- c bon, g demandé à ma calculatrice

Ça confirme mon calcul

par **Hiphigenie** » 28 Mar 2010, 19:31

Je viens juste de prendre l'exercice en cours et je confirme la réponse de Sa Majesté.

par **saralecompte** » 28 Mar 2010, 20:58

Je vous remercie vraiment à tous, mais j'ai refais ma dérivée seconde et je tombe sur la même chose, c est pas possible que l un d entre vous m envoi son raisonnement parce que je vous crois à 100% que vous avez juste mais je ne comprend plus rien :cry:

par **ned aero** » 28 Mar 2010, 21:02

Pour saralecompte, c'est les 3 dernières lignes de ton calcul de f" qqui sont incorrectes, tu prends un risque en factorisant par 1/;)

il vaut mieux factoriser par

(x-1)/(x+1)

ça aurait donné:

1/(x-1)² [ 2/(x-1)*;)(x-1)/(x+1) - 1/(x+1)²*

(x+1)/(x-1)]=

1/(x-1)² *;)(x-1)/(x+1)[ 2/(x-1) - 1/(x+1)² * (x+1)/(x-1)]

j'ai mis en bleu la factorisation "délicate"

ensuite, ça va tout seul jusqu'au résultat trouvé par Mathelot et Sa majesté

par **saralecompte** » 28 Mar 2010, 21:05

Hooo merci beaucoup Ned Aero, j vais regarder ca tout de suite j espère que ca va aller maintenant tu me sauves la vie :we:

par **saralecompte** » 28 Mar 2010, 21:17

Oui j ai fini de faire le calcul et je trouve enfin la réponse correcte je suis soulagé merci, maintenant j vais faire le tableau de signe ;)

par **ned aero** » 28 Mar 2010, 21:27

un exercice sur les dérivées est une chose infiniment petite dans quelque chose d'infiniment grand qu'est la vie, qui ne se résume d'ailleurs pas qu'aux maths ( heureusement...)

Bonne continuation

Etude de fonction

domaine de définition de sin3x

Qui est en ligne