Bonjour,
Je cherche à résoudre l'équation suivante :
-b/((1+e^(bx+a) )²(1+e^(dx+c))) e^(bx+a)-d/((1+e^(bx+a) )(1+e^(dx+c))²) = 0
J'aurai besoin d'une solution de la forme x=f(a,b,c,d) puisqu'après je réutilise cette solution avec différentes valeurs pour les paramètres a,b,c et d.
Est ce que cette équation est résolvable "à la main" ? Pour l'instant je n'ai pas réussi.
Quelqu'un aurait-il une idée comment faire ? Quel logiciel libre me conseillez-vous qui serait capable de résoudre ce genre d'équation ?
Toute aide est la bienvenue!
Merci beaucoup
Résolution d'équation
15 messages
- Page 1 sur 1
par Nightmare » 27 Jan 2010, 15:39
Ton équation me fait mal aux yeux et ces derniers n'ont vraiment pas envie de déchiffrer les parenthèses (à supposer qu'elles soient bien mises) pour la comprendre.
Avant de te conseiller un logiciel pour résoudre les équations, je te suggère un logiciel pour les écrire, présent sur ce site qui plus est : le LaTeX :lol3:
Avant de te conseiller un logiciel pour résoudre les équations, je te suggère un logiciel pour les écrire, présent sur ce site qui plus est : le LaTeX :lol3:
par SlowBrain » 27 Jan 2010, 23:52
Reporte toi à http://www.maths-forum.com/showthread.php?t=70548 sur ce forum pour le LaTeX for Dummies like me. Bonne nuit à tous!
par Lumino » 28 Jan 2010, 09:17
Bonjour,
Ne vous impatientez pas, la voici l'équation toute belle. Je suis néophyte en la matière donc j'espère que ça va marcher.
^2.(1+e^{d.x+c})}.e^{b.x+a}-frac{d}{(1+e^{b.x+a}).(1+e^{d.x+c})^2}.e^{d.x+c}= 0)
Ne vous impatientez pas, la voici l'équation toute belle. Je suis néophyte en la matière donc j'espère que ça va marcher.
par Lumino » 28 Jan 2010, 09:33
Bonjour
Je découvre ce langage mais je crois que c'est bon. (Je suis biologiste, soyez indulgent, je me débrouille en maths mais sans plus!!) Voici l'équation en plus jolie !
^2(1+e^{dx+c})}.e^{bx+a}+\frac{-d}{(1+e^{dx+c})^2(1+e^{bx+a})}.e^{dx+c} = 0)
Pour plus de précision, c'est la dérivée de cette fonction = \frac{1}{1+e^{bx+a}} \frac{1}{1+e^{dx+c}})
que je cherche à annuler pour trouver la valeur du maximum.
Voila. Si quelqu'un a une idée...
PS : merci SlowBrain pour le lien sur LaTex, ça m'a bien aidé
Je découvre ce langage mais je crois que c'est bon. (Je suis biologiste, soyez indulgent, je me débrouille en maths mais sans plus!!) Voici l'équation en plus jolie !
Pour plus de précision, c'est la dérivée de cette fonction
Voila. Si quelqu'un a une idée...
PS : merci SlowBrain pour le lien sur LaTex, ça m'a bien aidé
par SlowBrain » 28 Jan 2010, 10:10
Là ça devient bien plus simple quand tu te rappelles que 1/l'exponentielle est toujours positive et donc tu peux ignorer tes dénominateurs qui ne changent pas le signe de ton expression, puis 2/l'exponentielle a des propriétés algébriques confortables pour ce calcul donc 
=x+c-a})
lorsque l'on cherche à simplifier.
par Ben314 » 28 Jan 2010, 10:24
Une autre façon de trouver cette formule "plus simple" est d'écrire que f=1/g donc que f'=-g'/g² est du signe de -g'.
On a=b\,e^{bx+a}(1+e^{dx+c})+d\,e^{dx+c}(1+e^{bx+a}))
Le seul truc évident, c'est que si b et d sont de même signe, f est monotone sur R et que sa borne sup (sur R) est 1.
Par contre, si b et d sont de signe opposé, f est positive, tend vers 0 en +oo et en -oo donc atteint un Max quelque part. J'ai l'impression que l'on ne peut pas exprimer le x_max par une formule élémentaire dépendant de a,b,c,d...
On a
Le seul truc évident, c'est que si b et d sont de même signe, f est monotone sur R et que sa borne sup (sur R) est 1.
Par contre, si b et d sont de signe opposé, f est positive, tend vers 0 en +oo et en -oo donc atteint un Max quelque part. J'ai l'impression que l'on ne peut pas exprimer le x_max par une formule élémentaire dépendant de a,b,c,d...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
des formules magiques
par mathelot » 28 Jan 2010, 11:01
Bj,
=\frac{1}{1+e^{bx+a}} \, \frac{1}{1+e^{dx+c}})
On passe au log népérien et aux "arcs moitiés" pour faire apparaitre des
cosinus:
|)= -\left( \frac{b+d}{2}x+\frac{a+c}{2}+ln(cosh(\frac{bx+a}{2})) +ln(cosh(\frac{dx+c}{2})) +2 ln(2) \right))
en dérivant
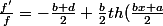+\frac{d}{2} th(\frac{dx+c}{2}))
les valeurs x qui annulent la dérivée f'(x) vérifient:
+\frac{d}{2} \, th(\frac{dx+c}{2})= \, \frac{b+d}{2})
pas de solutions si bd>0 car la tangente hyperbolique \in ]-1;1[)
On passe au log népérien et aux "arcs moitiés" pour faire apparaitre des
cosinus:
en dérivant
les valeurs x qui annulent la dérivée f'(x) vérifient:
pas de solutions si bd>0 car la tangente hyperbolique
où ça commence à chauffer....
par mathelot » 28 Jan 2010, 12:55
la valeur x qui annule la dérivée f'(x) vérifie:
re,
si l'on regarde la courbe représentative de la tangente hyperbolique ,
elle est quand même très particulière:
quasiment linéaire à l'origine puis constante égale à 1 ....
admettons qu'elle soit linéaire dans un voisinage de l'origine :zen:
l'équation (1) devient par linéarité:
la fonction th(), strictement croissante admet une fonction
réciproque
tous calculs faits, ça donne comme valeur approchée de la racine de f':
:ptdr: :ptdr:
remarque:
il est naturel de ne pas chercher de solution en x, dans un voisinage de l'infini.
par Lumino » 29 Jan 2010, 13:55
Bonjour,
Merci beaucoup pour toutes vos réponses. Je viens d'avoir confirmation que cette équation n'est pas résolvable. :triste:
En fait, la fonction f(x) est celle du modèle HOF dont je me sers pour ajuster mes données. J'obtiens les paramètres a, b, c et d quand j'ai ajusté ce modèle à mes données. Mais j'aurai voulu obtenir le maximum de la courbe (d'où l'équation de la dérivée de f(x) égale à 0). Maintenant je ne vois que comme autre solution que le calcul numérique de mon maximum. Le souci c'est que je cherche également un intervalle de confiance de ce maximum.
Si je n'avais pas eu le problème de l'équation, je rentre dans SAS ma formule du maximum en fonction de a, b, c et d et le logiciel me trouve et le maximum et l'intervalle de confiance de ce maximum par la delta method.
Mais là je suis coincée.
Je pense faire un bootstrap sur mes données pour trouver l'intervalle de confiance.
Mon problème de maths s'est transformé en problème de stats!
Voilà, vous savez le fin mot de l'histoire. Si quelqu'un a des idées ou un avis sur le boostrap ou quant à la méthode à employer, je prends!
Merci
Merci beaucoup pour toutes vos réponses. Je viens d'avoir confirmation que cette équation n'est pas résolvable. :triste:
En fait, la fonction f(x) est celle du modèle HOF dont je me sers pour ajuster mes données. J'obtiens les paramètres a, b, c et d quand j'ai ajusté ce modèle à mes données. Mais j'aurai voulu obtenir le maximum de la courbe (d'où l'équation de la dérivée de f(x) égale à 0). Maintenant je ne vois que comme autre solution que le calcul numérique de mon maximum. Le souci c'est que je cherche également un intervalle de confiance de ce maximum.
Si je n'avais pas eu le problème de l'équation, je rentre dans SAS ma formule du maximum en fonction de a, b, c et d et le logiciel me trouve et le maximum et l'intervalle de confiance de ce maximum par la delta method.
Mais là je suis coincée.
Je pense faire un bootstrap sur mes données pour trouver l'intervalle de confiance.
Mon problème de maths s'est transformé en problème de stats!
Voilà, vous savez le fin mot de l'histoire. Si quelqu'un a des idées ou un avis sur le boostrap ou quant à la méthode à employer, je prends!
Merci
par mathelot » 29 Jan 2010, 14:12
chère Madame,
Nous savions dès le début que votre équation n'était pas résolvable. Auriez vous l'extrême amabilité de rentrer la formule
indiquée plus haut (post #9) pour tester si celle-ci donne une approximation ,
certes prolétarienne, mais convenable tout de même, du résultat ?
Nous savions dès le début que votre équation n'était pas résolvable. Auriez vous l'extrême amabilité de rentrer la formule
indiquée plus haut (post #9) pour tester si celle-ci donne une approximation ,
certes prolétarienne, mais convenable tout de même, du résultat ?
par Lumino » 29 Jan 2010, 15:15
Je viens de tester et ça ne marche pas, ça tombe vraiment loin du maximum de ma distribution. :triste:
par Ben314 » 29 Jan 2010, 15:24
Ca ne m'étone que moyennement, vu que la fonction n'est "quasi linéaire" que dans un petit voisinage de 0. La méthode ne marche bien que si les valeurs de a,b,c,d donne une équation "proche de 0"
Pour trouver une approximation de x_o, tu peut (le plus concon) faire une dichotomie ou bien (j'ai l'impression que ça s'y prette parfaitement) utiliser la méthode des tangentes de Newton en partant de Uo=0 (cherche sur Google si tu ne connais pas, c'est pas trop complexe et, souvent, ça donne une trés bonne approximation en une dizaine d'itérations)
Pour trouver une approximation de x_o, tu peut (le plus concon) faire une dichotomie ou bien (j'ai l'impression que ça s'y prette parfaitement) utiliser la méthode des tangentes de Newton en partant de Uo=0 (cherche sur Google si tu ne connais pas, c'est pas trop complexe et, souvent, ça donne une trés bonne approximation en une dizaine d'itérations)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :