Isomorphismes de groupes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 14 Mar 2006, 18:24
par Anonyme » 14 Mar 2006, 18:24
Bonjour, j'aurai bien besoin d'aide sur cet exo, merci
Soient G,H,J des groupes tels qu'il existe un isomorphisme f de G dans HxJ
Je dois montrer que
"g qui appartient à G est un générateur de g " équivaut à "f(g) = (h,j) avec h un générateur de H et j un générateur de J"
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 14 Mar 2006, 18:28
par El_Gato » 14 Mar 2006, 18:28
Salut,
f est un isomorphisme de G dans H x J. H x J est muni de la structure canonique de groupe produit:
(h_2, j_2) = (h_1 h_2, j_1, j_2))
. Un isomorsphisme transporte les générateurs. Et un générateur du groupe produit a la forme indiquée.
-
Anonyme
 par Anonyme » 14 Mar 2006, 18:47
par Anonyme » 14 Mar 2006, 18:47
oui mais faut que je demontre qu'un ismorphisme transporte les générateurs, je suis pas censée le savoir, t'aurais pas une demonstration de ça?
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 14 Mar 2006, 19:00
par El_Gato » 14 Mar 2006, 19:00
 = (f(g))^n)
.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Mar 2006, 21:10
par yos » 14 Mar 2006, 21:10
Si g engendre G, alors f(g) engendre HXJ (est-ce clair?)
Posons f(g)=(h,j). Les puissances de f(g) vont donc décrire HXJ. C'est-à-dire que les
)
vont décrire HXJ. Et donc les

décrivent H et les
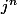
décrivent J.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
