Isomorphismes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Mar 2010, 13:03
par barbu23 » 11 Mar 2010, 13:03
Bonjour : :happy3:
Soit

un endomorphisme tel que :
 = M(\varphi) X $)
avec
 $)
la matrice associée à
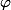
.
Par definition, l'endomorphisme transposée de
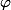
est par definition :

telle que :
 = ^t M(\varphi) L $)
avec :
 $)
la matrice associée à

.
Comment s'écrit :

dans la base

?
Merci d'avance ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Mar 2010, 13:07
par barbu23 » 11 Mar 2010, 13:07
 par alavacommejetepousse » 11 Mar 2010, 13:07
par alavacommejetepousse » 11 Mar 2010, 13:07
bonjour
rem la transposée se définit de cette manière pour une application linéaire quelconque pas seulement pour un endo
de façon simple
f : E-> F linéaire tf : F* ->E* u -> u°f
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Mar 2010, 13:12
par barbu23 » 11 Mar 2010, 13:12
Oui, c'est vrai, Merci ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Mar 2010, 13:19
par barbu23 » 11 Mar 2010, 13:19
Soit

un endomorphisme tel que :
 = M(\varphi) X $)
avec
 $)
la matrice associée à
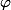
.
Par definition, l'endomorphisme transposée de
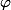
est par definition :

telle que :
 = ^t M(\varphi) L $)
avec :
 $)
la matrice associée à

.
Comment s'écrit :

dans la base

?

:


:


:
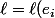 e_{i}^{*} $)
Et donc :
 \\ \ell(e_{i}) \\ \vdots \\ \ell(e_{i}) \end{pmatrix} $)
Maintenant, on sait comment s'écrit :

.
Par contre :
 = ( ^t \varphi (e_{1}^*) , ... , ^t \varphi (e_{n}^*) ) $)
N'est ce pas ?
C'est à dire l'espace vectoriel :

a pour base de colonnes :
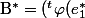 , ... , ^t \varphi (e_{n}^*) ) $)
N'est ce pas ? :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Mar 2010, 13:29
par barbu23 » 11 Mar 2010, 13:29
Moi, je prefère pas appeler
 $)
une matrice pour

, mais une base de l'espace d'arrivée de :

:

(

est surjective )
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
un endomorphisme tel que :
avec
la matrice associée à
.
est par definition :
telle que :
avec :
la matrice associée à
.
dans la base
?
:
:
: