Groupes et isomorphismes

[Axeldinh]

Bonjour,

Il y a une question à laquelle je n'arrive pas à répondre :

Sachant que est un groupe d'ordre 55 et qu'il possède 2 sous-groupes :
- de cardinal 5 avec .
- de cardinal 11 avec normal dans .

Montrer que est isomorphe à un sous-groupe de .

J'ai montré dans les questions précédentes que n'est pas cyclique et que .

Quelqu'un aurait une piste ? Merci d'avance !

[Ben314]

Salut,
C'est quoi que tu note ?
Et [G,G] ?

[Axeldinh]

Pour moi c'est le normalisateur de dans :

[Axeldinh]

Et [G,G] le sous groupe dérivé de G :

[Ben314]

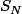
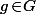
J'ai absolument rien regardé, mais si N est de cardinal 11 et distingué dans G, le premier truc qui vient à l'esprit pour construire une application de G dans , c'est de faire agir G sur N par conjugaison c'est à dire considérer l'application de G dans (groupe des bijections de N dans N) définie par pour tout et tout .
On vérifie facilement qu'elle est bien définie et que c'est bien un morphisme de groupe.
Reste à vérifier qu'elle est injective . . .