Bonjour,
(J'ai un clavier en qwerty, donc ne vous inquietez pas si les accents sont absents)
Alors pour resumer, ca fait deja plusieurs heures que je recherche une formule qui me calculera la distance entre le centre d un rectangle et un point d'un de ses cotes en fonction d'angle connu.
Je suis parti sur la piste la plus simple de placer mon rectangle dans un cercle trigo pour mieux analyser la situation puis j'ai vu qu'on pouvait facilement decouper chaque calcul comme une recherche d'hypothenus (Ca ce dit bien comme ca ?) dans un triangle rectangle.
Malheureusement je m'embrouille vraiment dans mes calculs et je commence vraiment a ... devenir fou !
C'est pourquoi je fais appel a vos esprits eclaires pour m'aider... surtout que sans pretention je suis vraiment trop fort en math (tout le monde aura compris que c'etait ironique).
Merci d'avance pour votre aide et merci d'avoir pris le temps de lire.
Si vous avez besoin d'informations complementaires, etc... faites le moi savoir.
Merci encore pour votre attention.
Cordialement,
Calcul de distance dans un rectangle
4 messages
- Page 1 sur 1
Oui c est tout aussi simple que ca ... malheureusement mon parcours atypique m a fait abandonner toutes notions en maths... j'avoue que manger des cos et sin etc... apres ... 6-7 ans sans y toucher... c'est un peu violant.
Si vraiment tu peux me mettre qq pistes, ca serait pas mal, sinon je regarderai ca demain a tete reposee.
Si vraiment tu peux me mettre qq pistes, ca serait pas mal, sinon je regarderai ca demain a tete reposee.
Si  est la demi largeur et
est la demi largeur et  la demi hauteur sur le dessin (c'est plus simple pour les calculs) alors,
la demi hauteur sur le dessin (c'est plus simple pour les calculs) alors,
Pour "petit", tu as
"petit", tu as ={cote\ adjacent\over hypothenuse}={a\over d}) donc
donc 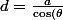}) .
.
On a aussi|={cote\ oppose\over cote\ adjacent}={x\over a}) donc le coté opposé est
donc le coté opposé est 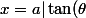|) et la première formule est valable tant que
et la première formule est valable tant que  c'est à dire tant que
c'est à dire tant que |\le{b\over a}) où, si tu préfère, que
où, si tu préfère, que  .
.
Si dépasse cette limite, tu fait un calcul similaire avec
dépasse cette limite, tu fait un calcul similaire avec  qui représente l'angle avec la demi droite verticale...
qui représente l'angle avec la demi droite verticale...
Pour
On a aussi
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

