Probabilité
14 messages
- Page 1 sur 1
Probabilité
Bonjour,
j'aimerais savoir comment résoudre ce type d'exercice :
Un programme comporte 10 erreurs. À chaque relecture, chaque erreur restante a une probabilité 1/4 d'être détectée et corrigée, de manière indépendante des autres erreurs. Combien de fois doit-on faire relire ce programme pour que la probabilité d'avoir corrigé les 10 erreurs soit supérieure à 0,99
Je pensais utiliser la fonction quantile mais je n'aboutis pas...
Merci d'avance de vos réponses
j'aimerais savoir comment résoudre ce type d'exercice :
Un programme comporte 10 erreurs. À chaque relecture, chaque erreur restante a une probabilité 1/4 d'être détectée et corrigée, de manière indépendante des autres erreurs. Combien de fois doit-on faire relire ce programme pour que la probabilité d'avoir corrigé les 10 erreurs soit supérieure à 0,99
Je pensais utiliser la fonction quantile mais je n'aboutis pas...
Merci d'avance de vos réponses
Salut Yos,
je trouve ton estimation bien optimiste. Ton calcul donne un résultat voisin de 24.
Par définition le nombre de relectures nécessaires pour corriger les 10 erreurs suit une loi de Pascal d'ordre 10 avec une probabilité de 1/4.
Son espérance est 10/(1/4)=40.
C'est un résultat évident compte tenu du fait que l'espérance de la v.a. "nombre de relecture pour corriger une erreur donnée" a pour espérance 4.
Pour information si X est le nombre de relecture ncéssaire pour corriger les 10 erreurs (quand elles sont corrigées on s'arrête)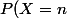={n-1 \choose 9}\frac{3^{n-10}}{4^n})
Je ne me sens pas de faire une somme assez longue de termes de ce type, mais je ne vois pas comment y échapper. :briques:
je trouve ton estimation bien optimiste. Ton calcul donne un résultat voisin de 24.
Par définition le nombre de relectures nécessaires pour corriger les 10 erreurs suit une loi de Pascal d'ordre 10 avec une probabilité de 1/4.
Son espérance est 10/(1/4)=40.
C'est un résultat évident compte tenu du fait que l'espérance de la v.a. "nombre de relecture pour corriger une erreur donnée" a pour espérance 4.
Pour information si X est le nombre de relecture ncéssaire pour corriger les 10 erreurs (quand elles sont corrigées on s'arrête)
Je ne me sens pas de faire une somme assez longue de termes de ce type, mais je ne vois pas comment y échapper. :briques:
Salut.
...et je le maintiens.
Une relecture corrige 2,5 erreurs en moyenne.
nuage a écrit:Salut Yos,
je trouve ton estimation bien optimiste. Ton calcul donne un résultat voisin de 24.
...et je le maintiens.
nuage a écrit:C'est un résultat évident compte tenu du fait que l'espérance de la v.a. "nombre de relecture pour corriger une erreur donnée" a pour espérance 4.
Une relecture corrige 2,5 erreurs en moyenne.
nuage a écrit:Pour information si X est le nombre de relecture ncéssaire pour corriger les 10 erreurs (quand elles sont corrigées on s'arrête)
Je ne me sens pas de faire une somme assez longue de termes de ce type, mais je ne vois pas comment y échapper. :briques:
bonjour
je n ai pas compris de quelle somme il s agi(rait)
Déjà on peut se ramener à un problème où il n'y a qu'une seule erreur dans l'énoncé en considérant qu'à chaque étape la probabilité de correction est la même pour chaque erreur et que ces variables sont indépendantes.
On veut donc P(tout corrigé) = P (erreur 1 corrigée)* P (erreur 2 corrigée) * ...
= P (erreur i corrigée)^10
donc P(tout corrigé) >0.99
=> P (erreur i corrigée) > 0.99^(1/10) ( ~ 0.999)
Ensuite le nombre de relecture pour une erreur suit une loi géométrique de param q=3/4
Sa fonction de répartition (proba de correction en moins de n étapes) est 1-q^n.
on veut donc le plus petit n tq 1-q^n >= 0.999
q^n <= 0.001
n >= ln(0.001) / ln(3/4)
soit n >= 24.01 donc n = 25 relectures
On veut donc P(tout corrigé) = P (erreur 1 corrigée)* P (erreur 2 corrigée) * ...
= P (erreur i corrigée)^10
donc P(tout corrigé) >0.99
=> P (erreur i corrigée) > 0.99^(1/10) ( ~ 0.999)
Ensuite le nombre de relecture pour une erreur suit une loi géométrique de param q=3/4
Sa fonction de répartition (proba de correction en moins de n étapes) est 1-q^n.
on veut donc le plus petit n tq 1-q^n >= 0.999
q^n <= 0.001
n >= ln(0.001) / ln(3/4)
soit n >= 24.01 donc n = 25 relectures
bonjour,
je trouve 25 en prenant 99% de sureté. Au test.
( P(X<=25)=99%) )
J'ai testé la méthode de pascal
f = nchoosek(nbEssais-1,9)*3^(nbEssais-10)/4^nbEssais
avec nbchoosek(nbEssais-1,9)=C_{9}^{nbEssais-1}
Et je trouve que ca vaut au plus 3,8005% pour n = 36
Donc j'ai tendance a dire que c'est faux. Par ailleurs je comprends pas pourquoi chercher le n tel que P(X=n), vu que la fonction que suit X est pas monotone... (jor P(X=n+1)<P(X=n))
Mais j'aimerais bien une explication concernant la loi de pascal, j'arrive pas a faire l'analogie avec la description chez bibmath.
Chez bibmath la description dit :
On lance une pièce de monnaie (truquée) dont la probabilité d'obtenir pile est p. On note X le nombre de lancers nécessaires pour obtenir le r-ième pile. Alors X suit une loi de Pascal de paramètres r et p.
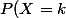 = C_{k-1}^{r-1} p^r(1-p)^{k - r})
On semble mettre r = 10 (la 10eme correction),p=3/4(la proba d'une correction), on a X qui donne le nombre de lectures pour la 10eme correction.
Seulement la proba d'une correction est-elle 3/4? Ici il s'agit de la lecture, pas d'une erreur en particulier?
je trouve 25 en prenant 99% de sureté. Au test.
( P(X<=25)=99%) )
J'ai testé la méthode de pascal
f = nchoosek(nbEssais-1,9)*3^(nbEssais-10)/4^nbEssais
avec nbchoosek(nbEssais-1,9)=C_{9}^{nbEssais-1}
Et je trouve que ca vaut au plus 3,8005% pour n = 36
Donc j'ai tendance a dire que c'est faux. Par ailleurs je comprends pas pourquoi chercher le n tel que P(X=n), vu que la fonction que suit X est pas monotone... (jor P(X=n+1)<P(X=n))
Mais j'aimerais bien une explication concernant la loi de pascal, j'arrive pas a faire l'analogie avec la description chez bibmath.
Chez bibmath la description dit :
On lance une pièce de monnaie (truquée) dont la probabilité d'obtenir pile est p. On note X le nombre de lancers nécessaires pour obtenir le r-ième pile. Alors X suit une loi de Pascal de paramètres r et p.
On semble mettre r = 10 (la 10eme correction),p=3/4(la proba d'une correction), on a X qui donne le nombre de lectures pour la 10eme correction.
Seulement la proba d'une correction est-elle 3/4? Ici il s'agit de la lecture, pas d'une erreur en particulier?
la vie est une fête 
Salut,
Je confirme la soluce de Yos.
On peut même calculer le "polynôme générateur") (dont le coeff. en
(dont le coeff. en 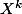 est la proba qu'il reste k erreurs aprés n relectures) :
est la proba qu'il reste k erreurs aprés n relectures) :
=\left(1-\left({3\over 4}\right)^n+\left({3\over 4}\right)^nX\right)^{10})
qui permet non seulement de vérifier que la proba. qu'aprés n relectures il reste 0 erreurs est bien de^n\right)^{10}) mais aussi de calculer si on veut la proba qu'il reste k=1,2,...,10 erreurs et de constater que, pour n fixé les différentes proba. (k=0,1,...,10) suivent une loie binomiale.
mais aussi de calculer si on veut la proba qu'il reste k=1,2,...,10 erreurs et de constater que, pour n fixé les différentes proba. (k=0,1,...,10) suivent une loie binomiale.
Par contre, je ne voie aucune loie de Pascal ici...
Je confirme la soluce de Yos.
On peut même calculer le "polynôme générateur"
qui permet non seulement de vérifier que la proba. qu'aprés n relectures il reste 0 erreurs est bien de
Par contre, je ne voie aucune loie de Pascal ici...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
