Valeur d'adhérence d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 18:36
par AMA112 » 06 Déc 2009, 18:36
D'accord! Ok merci beaucoup!
Passons à la question
c).
Pouvez-vous m'aider pour montrer que
\in[-1;1]\cap[y-1,y+1]\})
est infini?
 par alavacommejetepousse » 06 Déc 2009, 18:45
par alavacommejetepousse » 06 Déc 2009, 18:45
on a deux versions équivalentes de G dense dans [-1,1]
1 pour tout l de [-1,1] il existe une suite gn de G qui converge vers l
(cest celle que j ai utilisée)
2 pour tout y de [-1,1] G rencontre tout voisinage ouvert de y
2 étant équivalent à
2' pour tout y de [-1,1] G rencontre tout voisinage ouvert de y en une infinité de points.
sais tu faire 1=>2? et 2=> 2' ?
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 19:00
par AMA112 » 06 Déc 2009, 19:00
Non, je ne vois pas trop comment montrer ces implications...
D'ailleurs je ne comprend pas trop "G rencontre tout voisinage ouvert de y"
Ca veut dire que G inter un voisinage de y est non vide?
 par alavacommejetepousse » 06 Déc 2009, 19:09
par alavacommejetepousse » 06 Déc 2009, 19:09
oui
donc 1=>2 on suppose 1
soit y ds [-1,1] et V = ]y-a,y+a[ il existe une suite de G qui converge vers y donc à partir d'un certain rang gn est dans V donc V interG est non vide
d'où 2
2=>2' on suppose 2 montrons 2' par l'absurde
on aurait ds le cas contraire un certain intervalle ]a,b[ inclus dans [-1,1]non vide d'intersection avec G finie d'où un autre intervalle (faire un dessin)
]a'b'[ d'intersection vide avec G
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 19:39
par AMA112 » 06 Déc 2009, 19:39
D'accord j'ai compris, merci infiniment.
Voici mon ébauche pour le deuxième point du
c)On veut construire par récurrence
})_{n\in\mathbb{N}})
extraite de u telle que
}\in A_n=\{n\in\mathbb{N} / cos(n)\in[-1;1]\cap[y-\frac{1}{n+1},y+\frac{1}{n+1}]\})
, où

est infini.
Pour n=0, comme
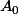
est infini, on fixe un élément noté
})
Soit

, supposons construit

infini.
Mais après je ne sais pas comment "découper"

pour avoir
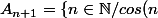\in[-1;1]\cap[y-\frac{1}{n+2},y+\frac{1}{n+2}]\})
infini.
Est-ce que c'est juste?
 par alavacommejetepousse » 06 Déc 2009, 19:56
par alavacommejetepousse » 06 Déc 2009, 19:56
une chose m ennuie le dernier point du c est exactement ce que j ai utilisé comme définition de la densité j en déduis que la logique de l exo était d utiliser le 2 pour la densité et donc ce que Ben te proposait...
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 20:04
par AMA112 » 06 Déc 2009, 20:04
Justement, je n'avais pas bien compris ce que Ben314 proposait...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités