Valeur d'adhérence d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 05 Déc 2009, 21:56
par AMA112 » 05 Déc 2009, 21:56
Bonjour,
J'ai un exo dont voici l'énoncé:
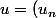_{n\in\mathbb{N}}\in\mathbb{R}^{\mathbb{N}})
, a est une valeur d'adhérence de u s'il existe une suite extraite v de u convergeant vers a.
On note
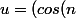)_{n\in\mathbb{N}})
et on veut montrer que l'ensemble des valeurs d'adhérence de u est [-1;1].
On rapelle que tout sous-groupe G de
)
non réduit à {0} est soit dense dans

, soit de la forme

, où

.
a) Soit
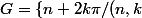\in\mathbb{Z}^2\})
, montrer que G est un sous groupe de
)
.
Pour cette question pas de problème.b) En déduire que
 / n\in\mathbb{Z}\})
est dense dans [-1;1], puis que
 / n\in\mathbb{N}\})
est dense dans [-1;1].
Là j'ai un peu de mal pour la première partie. Pour la seconde partie il faut utiliser la parité de cos je suppose.c) Soit

.
Montrer que
\in[-1;1]\cap[y-1,y+1]\})
est infini.
Construire par récurrence une suite extraite de u convergeant vers y.
Conclure.
Pour ces trois questions je n'ai aucune idée.Dans l'attente, merci.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2009, 22:25
par Ben314 » 05 Déc 2009, 22:25
Bonsoir,
pour le a), as-tu pensé à répondre à la question qui n'est pas posée mais suggérée par le préliminaire :
G est il dense ou de la forme sZ ?
Indic : à mon avis pour la réponse, il faut savoir que PI n'est pas un quotient (ce n'est pas super simple à démontré).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 11:03
par AMA112 » 06 Déc 2009, 11:03
Oui j'ai pensé à ça: G est dense dans R (car pi est irrationnel). Mais je suis quand meme bloqué...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2009, 11:41
par Ben314 » 06 Déc 2009, 11:41
A ce moment là, la seule "petite" astuce, c'est de constater que, comme cos est 2-pi périodique,
=cos(G))
(images directes) et de conclure en utilisant la continuité de la fonction cos et la densité de G dans R...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 11:58
par AMA112 » 06 Déc 2009, 11:58
en utilisant la continuité de la fonction cos et la densité de G dans R...
C'est justement cette étape que je ne sais pas rédiger...
Merci.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2009, 12:08
par Ben314 » 06 Déc 2009, 12:08
Il existe un théorème qui te "vend" direct le résultat, mais c'est pas trés compliqué "à la main" :
Montrer que cos(G) est dense dans [0,1] revient à montrer que tout ouvert non vide de [0,1] rencontre cos(G).
Soit U un tel ouvert. Que peut tu dire de
)
?
Qu'en déduit tu ? (vu que G est dense dans R)
Conclusion.
P.S. si la densité "avec les ouverts" te pose problème, prend à la place de U un ]xo-epsilon,xo+epsilon[...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 13:00
par AMA112 » 06 Déc 2009, 13:00
En effet, je ne connais pas la densité avec les ouverts, est-ce que c'est pareil que les voisinages (qu'on a vu en cours) ?
Ben314 a écrit:Soit U un tel ouvert. Que peut tu dire de
)
?
Je ne vois pas...
)
est non vide?
Qu'en déduit tu ? (vu que G est dense dans R)
Conclusion.
Peux-tu expliquer un peu plus? Parce que je ne comprend pas trop..
Merci.
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 16:38
par AMA112 » 06 Déc 2009, 16:38
svp quelqu'un?
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 17:08
par AMA112 » 06 Déc 2009, 17:08
Bonsoir alavacommejetepousse,
Je veux montrer la question b)
 par alavacommejetepousse » 06 Déc 2009, 17:11
par alavacommejetepousse » 06 Déc 2009, 17:11
bon
G est dense dans R car pi irrationnel
cos est continue donc
cos(G) est dense dans cos(R) (ça va ça?) et le résultat
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 17:14
par AMA112 » 06 Déc 2009, 17:14
cos est continue donc
cos(G) est dense dans cos(R)
C'est justement ce passage que je n'arrive pas à démontrer.
 par alavacommejetepousse » 06 Déc 2009, 17:20
par alavacommejetepousse » 06 Déc 2009, 17:20
bon
visiblement tu as du mal avec les ouverts je fais donc avec les suites
pour l dans [-1,1] = cos(R) il existe x dans r tel que l = cos(x)
comme G est dense dans R il existe (gn) une suite de G qui converge vers x et comme cos est continue ,cos(gn) converge vers cos(x) = l

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2009, 17:23
par Ben314 » 06 Déc 2009, 17:23
Alavacommejetepousse utilise "direct" le théorème...
Pour le démontrer, même en prenant la définition de dense avec les voisinages, ca tient 3 lignes :
Soit

et
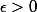
.
Il faut montrer que
\cap ]x_o-\epsilon,x_o+\epsilon[)
est non vide....
Essaye de l'écrire : ça... coule de source...
P.S. où avec les suites comme le suggère alavacommejetepousse : on passe de 3 lignes à... 1 ligne.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 17:29
par AMA112 » 06 Déc 2009, 17:29
Le théorème en question c'est bien: G est dense dans R ssi pour tout x de R il existe une suite d'éléments de G convergeant vers x?
Si oui on l'a vu en cours ce théorème, donc on peut l'utiliser.
Y'a juste un truc que je ne saisis pas: pourquoi utilise-t-on le fait que cos soit continue?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Déc 2009, 17:57
par Nightmare » 06 Déc 2009, 17:57
Quid de cos(p) avec p décrivant l'ensemble des nombres premiers? :lol3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2009, 18:01
par Ben314 » 06 Déc 2009, 18:01
c'est forcément dense (sinon, ca se saurait)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 06 Déc 2009, 18:09
par ffpower » 06 Déc 2009, 18:09
Si

est irrationnel, alors les

sont équirépartis modulo 1
Mais il parait que la preuve est assez hard...
-
AMA112
- Membre Naturel
- Messages: 16
- Enregistré le: 01 Oct 2008, 16:13
-
 par AMA112 » 06 Déc 2009, 18:23
par AMA112 » 06 Déc 2009, 18:23
Quelqu'un pour mon pb?
il existe (gn) une suite de G qui converge vers x et comme cos est continue ,cos(gn) converge vers cos(x) = l
Y'a juste un truc que je ne saisis pas: pourquoi utilise-t-on le fait que cos soit continue?
Y'a juste à utiliser la caractérisation séquentielle de la limité et c'est fini non?
 par alavacommejetepousse » 06 Déc 2009, 18:32
par alavacommejetepousse » 06 Déc 2009, 18:32
bon
pour f ayant une limite l au point x
pour (gn) une suite qui tend vers x on a f(gn) qui tend vers l
ici l = cos x
si f n a pas de limite au point x c est pas vrai a priori
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
