Algèbre orbites

[kopou]

bonjour j'aurais besoin d'un coup de main pour les questions sur les orbites merci d'avance à vous tous
voici l'énoncé
soit A un anneau on note A* le groupe multiplicatif des éléments inversibles de A
1)montrer que l'application phi: A* x A dans A qui à (x,a) associe xa est une opération du groupe A* sur l'ensemble A
2)quelles sont les orbites respectives de 0 et de 1 pour cette opération?
3)montrer que A est un corps si et seulement si le nombre d'orbites de cette opération est égal à 2
4)on suppose que A=Z/12Z déterminer les éléments de groupe de A* et vérifier que ce groupe est isomorphe à Z/2Z x Z/2Z
5) déterminer toutes les orbites de l'ensemble A sous l'action de A*

[Arkhnor]

Bonjour.

Pour la 1), il suffit de montrer que les propriétés qui définissent une action de groupe sont vérifiées. Les connais-tu ?

2) Ecris la définition de l'orbite d'un élément, et explicite un peu ce que ça donne ...

3) La question 2) va être utile.

4) Ce n'est que du calcul, soit tu ne connais pas de résultats particuliers sur les inversibles des anneaux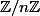 , et tu dresses la table de multiplication de 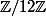, et tu listes les éléments inversibles, soit tu sais que les inversibles de l'anneau 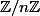sont les 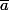tels que , et donc dans ce cas, tu listes les entiers entre 1 et 11 qui sont premiers avec 12.

Ensuite pour l'isomorphisme, soit tu le trouves à la main, en regardant les tables des deux groupes, soit tu observes que est un groupe d'ordre 4, dont tous les éléments autre que le neutre sont d'ordre 2, et qu'un tel groupe est nécessairement isomorphe à

5) La encore, ce n'est que du calcul, encore faut-il avoir compris ce qu'est une orbite.

Tu devrais dire clairement ce que tu as tenté dans cet exercice, et ce que tu ne comprends pas.

[kopou]

bonjour
pour la question 1)et 4) c'est bon
pour la 2) j'ai mis orb(0) = {x.0 / x appartient à A*}
orb(1) = {x.1 / x appartient à A*}
par contre pour la 3) et 5) je ne vois pas trop comment commencé
merci

[Arkhnor]

Et que valent 0.x et 1.x dans un anneau ? ...

Pour la 3), une fois que t'auras fini la 2), ca ira mieux, je pense.

Pour la 5), si j'ai bien compris, on raisonne toujours avec l'anneau
Tu prend donc chaque élément, et tu calcules son orbite, en utilisant la définition.