Matrice symétrique - forme quadratique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 24 Aoû 2009, 18:08
par MacManus » 24 Aoû 2009, 18:08
Bonsoir ! :happy:
Soient E un E.V. euclidien de dimension 4 rapporté à une base orthonormée B=(e1,e2,e3,e4). On considère la matrice
symétrique à coefficients réels définie par :

On suppose que l'endomorphisme associé est
non bijectifJ'ai plusieurs questions concernant cette matrice M.
1) Quel est le rang de M ? ( rg(M)=2 ? )
2) Comment puis-je calculer com(M), la commatrice de M (je connais la formule
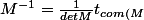})
mais est-elle bien adaptée ici ?)
J'ai une question peut-être bête : peut-on dire que toute matrice symétrique réelle est inversible ? eh bien je pense que NON
Merci beaucoup !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2009, 18:23
par girdav » 24 Aoû 2009, 18:23
Bonjour.
Pour la comatrice on a la méthode bourrin qui consiste à calculer le mineur (le déterminant avec la colonne et la ligne correspondant "barrées".
J'ai une question peut-être bête : peut-on dire que toute matrice symétrique réelle est inversible ? eh bien je pense que NON
Je crois aussi:

doit être un conte-exemple.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 24 Aoû 2009, 18:28
par skilveg » 24 Aoû 2009, 18:28
Salut,
Pour la 1), je crois qu'il y a plein de cas à distinguer:

ou non,

ou non,
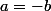
ou non. Tu n'as pas plus d'hypothèses sur

et

? ça permettrait peut-être de calculer la comatrice à la main (si la matrice est de rang inférieur à 2, elle est nulle).
Pour la 3) (qui vient d'être effacée...): oui.
Pour le coup des matrices symétriques inversibles, la matrice nulle est un contre-exemple encore meilleur.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 24 Aoû 2009, 18:29
par MacManus » 24 Aoû 2009, 18:29
Ok merci girdav je vais calculer cette commatrice :)
pour le rang en revanche je ne suis pas très certain...
il y a bien des conditions sur les réels a et b mais dans des questions prédédentes de mon sujet et pas pour cette question précisément!!
oui j'ai trouvé la réponse à la question 3 que je viens d'effacer!
Merci pour vos exemples.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 24 Aoû 2009, 18:35
par skilveg » 24 Aoû 2009, 18:35
Je te déconseille de calculer brutalement la comatrice, ça fait quand même 16 déterminants 3*3... Essaie plutôt d'utiliser le rang: si c'est 2, la comatrice est nulle, si c'est 3, elle est de rang inférieur à 1, avec des lignes dans le noyau de la matrice, et il suffit de calculer 4 déterminants 3*3.
Tu es vraiment sûr que tu n'as pas plus d'infos sur a et b?
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 24 Aoû 2009, 18:38
par MacManus » 24 Aoû 2009, 18:38
Oui c'est plus intelligents je pense. Merci skilveg
Si je viens de voir la condition ;)a;);) ;)b;) (excusez-moi)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2009, 18:45
par girdav » 24 Aoû 2009, 18:45
MacManus a écrit:Oui c'est plus intelligents je pense. Merci skilveg
Si je viens de voir la condition

a;);)

b;) (excusez-moi)
C'est plus rapide que de calculer les 16 déterminants! On peut donc établir que le rang est plus grand que

. Reste à montrer que ça ne peut pas être

.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 24 Aoû 2009, 18:49
par skilveg » 24 Aoû 2009, 18:49
Si, c'est 3, je crois: le déterminant du mineur principal en haut à gauche vaut
^2)
(si je ne me suis pas planté).
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 24 Aoû 2009, 18:50
par MacManus » 24 Aoû 2009, 18:50
Oui d'accord je vois. merci à vous deux. (je ne voulais pas dire que tu n'étais pas inteliligent girdav en tout cas :lol3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2009, 19:02
par girdav » 24 Aoû 2009, 19:02
MacManus a écrit:Oui d'accord je vois. merci à vous deux. (je ne voulais pas dire que tu n'étais pas inteliligent girdav en tout cas :lol3:
Vu le festival que j'ai fais...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
