Allez,encore un petit exo d algebre lin avant de partir en vacances.. :we:
Que dire d une matrice carrée A inversible dont tous les coefficients sont positifs, et dont tous les coefficients de l inverse sont aussi positifs?
Matrices a coefficients positifs
9 messages
- Page 1 sur 1
Ah c'est bon, je crois que je l'ai. On a 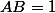 avec
avec  et
et  à coefficients positifs; en regardant ce que ça donne en termes de coefficients, ça veut dire que pour
à coefficients positifs; en regardant ce que ça donne en termes de coefficients, ça veut dire que pour 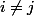 et
et  quelconque,
quelconque,  . En prenant pour tout
. En prenant pour tout  un
un  tel que
tel que  (il existe sinon
(il existe sinon  ne serait pas inversible), cela montre que
ne serait pas inversible), cela montre que  pour chaque
pour chaque 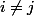 . Donc
. Donc  est bien une espèce de matrice de permutation. La réciproque est facile.
est bien une espèce de matrice de permutation. La réciproque est facile.
(EDIT: d'ailleurs ça résout le problème de la matrice dans) positive et à puissances bornées: son inverse est une de ses puissances, donc à coefficients positifs; et une pseudo-matrice de permutation à coefficients entiers est (en prenant le déterminant) une vraie matrice de permutation.)
positive et à puissances bornées: son inverse est une de ses puissances, donc à coefficients positifs; et une pseudo-matrice de permutation à coefficients entiers est (en prenant le déterminant) une vraie matrice de permutation.)
(EDIT: d'ailleurs ça résout le problème de la matrice dans
Bien joué,c est encore plus simple que ce que j avais fait
 plutot
plutot
Pour etre precis,produit d une permutation et d une diagonale
Crois le ou non,j avais meme pas fait le rapprochement entre les 2 exos lol.Du coup,ca donne aussi une demo plus simple de cet exo que celle que j avais^^
espèce de matrice de permutation
Pour etre precis,produit d une permutation et d une diagonale
(EDIT: d'ailleurs ça résout le problème de la matrice dans \mathrm{GL}_n(\mathbb{Z}) positive et à puissances bornées: son inverse est une de ses puissances, donc à coefficients positifs; et une pseudo-matrice de permutation à coefficients entiers est (en prenant le déterminant) une vraie matrice de permutation.)
Crois le ou non,j avais meme pas fait le rapprochement entre les 2 exos lol.Du coup,ca donne aussi une demo plus simple de cet exo que celle que j avais^^
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
