Nobre premiers entre eux
17 messages
- Page 1 sur 1
nobre premiers entre eux
bonjour dans mon dm, je ne arrive pas montrer que r et s sont premiers entre eux
Montrer quil existe r et s entiers premier entre eux tel que d/r²+s² et que le quotient q de r²+s² par d soit strictement inférieur à d, si d>2.
Montrer quil existe r et s entiers premier entre eux tel que d/r²+s² et que le quotient q de r²+s² par d soit strictement inférieur à d, si d>2.
je ne comprend pas la question 2.
Le but est montrer que si n=a²+b² avec (a,b)premier entre eux et si d /n, alors d est aussi une somme de 2 carrés
1) vérifiez ceci sur quelque exemple
2) dans les hypothèses ci- dessus, soit d un diviseur de n.
Montrer quil existe r et s entiers premier entre eux tel que d/r²+s² et que le quotient q de r²+s² par d soit strictement inférieur à d, si d>2.
3) montrer qu alors, il existe c et e premiers entre eux tel que q/c²+e² que le quotient de c²+e² par q, noté f, soit strictement inférieur à q , si q>2et que re-sc soit divisible par q aussi que rc+se.
4) en déduire quil existe a1 et b1 premier entre eux, tel que d/a1+b1, le quotient a1+b1 par d étant strictement inférieur à q.
5) en deduire que d ou 2d de la forme k²+l², k e tl premières entre eux
Le but est montrer que si n=a²+b² avec (a,b)premier entre eux et si d /n, alors d est aussi une somme de 2 carrés
1) vérifiez ceci sur quelque exemple
2) dans les hypothèses ci- dessus, soit d un diviseur de n.
Montrer quil existe r et s entiers premier entre eux tel que d/r²+s² et que le quotient q de r²+s² par d soit strictement inférieur à d, si d>2.
3) montrer qu alors, il existe c et e premiers entre eux tel que q/c²+e² que le quotient de c²+e² par q, noté f, soit strictement inférieur à q , si q>2et que re-sc soit divisible par q aussi que rc+se.
4) en déduire quil existe a1 et b1 premier entre eux, tel que d/a1+b1, le quotient a1+b1 par d étant strictement inférieur à q.
5) en deduire que d ou 2d de la forme k²+l², k e tl premières entre eux
non avant j'ai I)
I) 1) montrer que pour tout couple (u,v) appartient N* N*,il existe z et w tel que u=vz+w , lwl<= lvl/2 z,w entiers
2)soit a et b 2 entier donnés et d appartient N*montrer quil exsite r et s premiers entre eux et un entier t tel que :
a=dk+tr , ltrl<=d/2
b=dk+ts ltsl<=d/2 ket k entiers
3) factoriser la quantité (rb-sa)²+(ra+sb)²
I) 1) montrer que pour tout couple (u,v) appartient N* N*,il existe z et w tel que u=vz+w , lwl<= lvl/2 z,w entiers
2)soit a et b 2 entier donnés et d appartient N*montrer quil exsite r et s premiers entre eux et un entier t tel que :
a=dk+tr , ltrl<=d/2
b=dk+ts ltsl<=d/2 ket k entiers
3) factoriser la quantité (rb-sa)²+(ra+sb)²
Salut.
Hier j'ai répondu trop vite dans le dernier message : en fait r est s sont premiers entre eux car on l'a prouvé dans la partie 1.
Il est essentiel de voir que la partie 2 (question 2) se fait avec la partie 1 (question 2).
L'égalité n=a²+b²=(dk+tr)²+(dk'+ts)²=d(...)+t²r²+t²s² que j'ai écrite utilise les écritures de a et b obtenues dans cette partie 1.
As-tu compris pourquoi d|r²+s² ?
Pour la fin de la question 2 : r²+s²=dq. Si on avait q>=d, alors on aurait r²+s²>=d², donc t²r²+t²s²>=t²d²>=d² (en effet t est non nul, sinon d diviserait a et b, ce qui ne se peut pas car d>2 et a étranger à b). L'inégalité t²r²+t²s²>=d² est impossible car |tr[<d/2 et |ts|<d/2. D'où la contradiction et donc le fait que q<d.
Hier j'ai répondu trop vite dans le dernier message : en fait r est s sont premiers entre eux car on l'a prouvé dans la partie 1.
Il est essentiel de voir que la partie 2 (question 2) se fait avec la partie 1 (question 2).
L'égalité n=a²+b²=(dk+tr)²+(dk'+ts)²=d(...)+t²r²+t²s² que j'ai écrite utilise les écritures de a et b obtenues dans cette partie 1.
As-tu compris pourquoi d|r²+s² ?
Pour la fin de la question 2 : r²+s²=dq. Si on avait q>=d, alors on aurait r²+s²>=d², donc t²r²+t²s²>=t²d²>=d² (en effet t est non nul, sinon d diviserait a et b, ce qui ne se peut pas car d>2 et a étranger à b). L'inégalité t²r²+t²s²>=d² est impossible car |tr[<d/2 et |ts|<d/2. D'où la contradiction et donc le fait que q<d.
bonjour merci beaucoup por votre reponse j'ai reuissit la question 2)
je fais 3) question je voulais savoir si c'est bon
ii- 3)montrer qu alors, il existe c et e premiers entre eux tel que q/c²+e² que le quotient de c²+e² par q, noté f, soit strictement inférieur à q , si q>2et que re-sc soit divisible par q aussi que rc+se.
reponse :dans I-3) il faut factoriser (re-sc)²+(rc+se)²
je trover (re-sc)²+(rc+se)²=(r²+s²)(c²+e²).
or c²+e²=((re-sc)²+(rc+se)²)/(r²+s²)
or c²+e²=qf
qf==((re-sc)²+(rc+se)²)/qd
donc (re-sc) et (rc+se)sont divisible par q
je fais 3) question je voulais savoir si c'est bon
ii- 3)montrer qu alors, il existe c et e premiers entre eux tel que q/c²+e² que le quotient de c²+e² par q, noté f, soit strictement inférieur à q , si q>2et que re-sc soit divisible par q aussi que rc+se.
reponse :dans I-3) il faut factoriser (re-sc)²+(rc+se)²
je trover (re-sc)²+(rc+se)²=(r²+s²)(c²+e²).
or c²+e²=((re-sc)²+(rc+se)²)/(r²+s²)
or c²+e²=qf
qf==((re-sc)²+(rc+se)²)/qd
donc (re-sc) et (rc+se)sont divisible par q
Ben je crois que c'est pas bon.
La factorisation de la partie 1, question 3 est OK.
Mais ensuite je crois que tu dois réappliquer le résultat obtenu pour (a,b,d) au triplet (r,s,q) car on a les mêmes hypothèses pour ce second triplet.
A la fin, ton calcul montre que q (et même q²) divise (r²+s²)(c²+e²), donc il divise (re-sc)²+(rc+se)². Mais on ne peut pas en déduire directement que q divise chacun des deux termes. Je dois rater quelquechose. Si j'ai le temps je regarderai ce soir.
A moins qu'un autre se dévoue?
La factorisation de la partie 1, question 3 est OK.
Mais ensuite je crois que tu dois réappliquer le résultat obtenu pour (a,b,d) au triplet (r,s,q) car on a les mêmes hypothèses pour ce second triplet.
A la fin, ton calcul montre que q (et même q²) divise (r²+s²)(c²+e²), donc il divise (re-sc)²+(rc+se)². Mais on ne peut pas en déduire directement que q divise chacun des deux termes. Je dois rater quelquechose. Si j'ai le temps je regarderai ce soir.
A moins qu'un autre se dévoue?
Bonjour.
Pour la question 3), il faut tout écrire explicitement :
Comme ,
,  et
et  vérifient les mêmes hypothèses que
vérifient les mêmes hypothèses que  ,
,  et
et  dans la question précédente, on peut écrire
dans la question précédente, on peut écrire 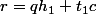 et
et  avec
avec  qui vérifient toutes les bonnes hypothèses. On a alors:
qui vérifient toutes les bonnes hypothèses. On a alors:
) qui est bien un multiple de
qui est bien un multiple de  et
et
+t_1(e^2+c^2)) qui est un multiple de
qui est un multiple de  car
car  .
.
Je passe à la question 4).
A bientôt
Pour la question 3), il faut tout écrire explicitement :
Comme
Je passe à la question 4).
A bientôt
Voilà,
La question 4) telle que tu l'as écrite ne convient pas. Il faut sans doute lire :
4) En déduire qu'il existe et
et  premiers entre eux, tels que
premiers entre eux, tels que  , le quotient de
, le quotient de  par
par  étant strictement inférieur à
étant strictement inférieur à  .
.
D'après la question 3), on peut écrire :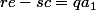 et
et 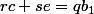 . La factorisation du I3) peut maintenant s'écrire:
. La factorisation du I3) peut maintenant s'écrire:
^2+(qb_1)^2=(r^2+s^2)(c^2+e^2)=q^2df) .
.
En simplifiant par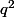 , on obtient
, on obtient
 , ce qui prouve à la fois que
, ce qui prouve à la fois que  et que le quotient (c'est-à-dire
et que le quotient (c'est-à-dire  ) est strictement inférieur à
) est strictement inférieur à  .
.
Reste à voir que et
et  sont bien premiers entre eux, mais je n'y arrive pas pour l'instant.
sont bien premiers entre eux, mais je n'y arrive pas pour l'instant.
A+
La question 4) telle que tu l'as écrite ne convient pas. Il faut sans doute lire :
4) En déduire qu'il existe
D'après la question 3), on peut écrire :
En simplifiant par
Reste à voir que
A+
merci beaucoup pour votre reponses
j'ai reuissit à demontrer a1 et b1 sont premiers entre eux mais bloqué dans 5eme question je n'est pas bien compis la question
5) en déduire que d ou 2d de la forme k²+l², k et l premier entre eux
vous pouvez donner des idées pour repondre 6éme question
6)en utilisan t héridité l²+k²=2(((k+l)/2)²+((k-l)/2)²)
montrer que d est une somme de 2 carrés
merci beaucoup pour aide
j'ai reuissit à demontrer a1 et b1 sont premiers entre eux mais bloqué dans 5eme question je n'est pas bien compis la question
5) en déduire que d ou 2d de la forme k²+l², k et l premier entre eux
vous pouvez donner des idées pour repondre 6éme question
6)en utilisan t héridité l²+k²=2(((k+l)/2)²+((k-l)/2)²)
montrer que d est une somme de 2 carrés
merci beaucoup pour aide
Bonsoir.
Peux-tu me donner ta démonstration de et
et  premiers entre eux ? J'ai vraiment séché sur cette question.
premiers entre eux ? J'ai vraiment séché sur cette question.
Pour la question 5) on se sert de ce qui précède : parmi tous les nombres que
que  divise (avec
divise (avec  et
et  premiers entre eux), tu en prends un qui rend le quotient
premiers entre eux), tu en prends un qui rend le quotient  minimal. Si
minimal. Si  , la question précédente nous montre qu'on peut trouver
, la question précédente nous montre qu'on peut trouver  et
et  tels que le quotient
tels que le quotient  soit strictement plus petit que
soit strictement plus petit que  . Ceci contredit la minimalité supposée de
. Ceci contredit la minimalité supposée de  .
.
On en déduit que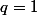 ou
ou 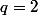 . Dans le premier cas, on a
. Dans le premier cas, on a  et dans le deuxième, c'est
et dans le deuxième, c'est  .
.
Voilà et peut-être à plus tard pour la question 6) (que je n'ai pas bien comprise à la première lecture (as-tu recopié exactement les mots de l'énoncé ?)).
Peux-tu me donner ta démonstration de
Pour la question 5) on se sert de ce qui précède : parmi tous les nombres
On en déduit que
Voilà et peut-être à plus tard pour la question 6) (que je n'ai pas bien comprise à la première lecture (as-tu recopié exactement les mots de l'énoncé ?)).
Bonjour
jai montrer a1 et b1 sont premier entre eux en utilisant question 2 d/r²+s² et d/a1+b1 donc jai appliqué le même règle à a1 et b1 donc :
a=dj1+ta1
b=dj2+tb& puis je pose x=a1t et y=b1t
t=pgcd(x,y)
t=pgcd (ta1, tb1)
t=tpgcd(a1,b1)
1=pgcd(a1,b1)
donc a1 et b1 sont premier entre eux
pour la question 6 jai écrit ce qui est donné dans lénoncé .
merci beaucoup pour votre réponses aux questions précédant
jai montrer a1 et b1 sont premier entre eux en utilisant question 2 d/r²+s² et d/a1+b1 donc jai appliqué le même règle à a1 et b1 donc :
a=dj1+ta1
b=dj2+tb& puis je pose x=a1t et y=b1t
t=pgcd(x,y)
t=pgcd (ta1, tb1)
t=tpgcd(a1,b1)
1=pgcd(a1,b1)
donc a1 et b1 sont premier entre eux
pour la question 6 jai écrit ce qui est donné dans lénoncé .
merci beaucoup pour votre réponses aux questions précédant
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
