Nombre premiers entre eux et congruence

[ArtyB]

Bonjour,

Je bloque sur cet exercice. J'ai fait la première question mais ne suis pas sûr de mon raisonnement et n'ai aucune idée pour la seconde. Si vous avez des pistes/corrections je suis preneur,

Merci,

Cordialement,

Arty

2). Soit a un entier naturel impair, non congru à 5 modulo 10.
2.1) Montrer que a est premier avec 100.
2.2) Pour tout entier naturel n multiple de 40, en déduire le reste de la division euclidienne de
an par 100.


2.1) Comme a est impair et non congru à 5 modulo 10, a ne se termine pas par 5 (mais par 1, 3, 7 ou 9), et n'est donc pas divisible par 5 (tous les multiples impairs de 5 se terminent par un 5).
Les seuls nombres impairs qui divisent 100 se terminent tous par un 5 sauf 1.
(Si a divise 100 alors a=1 et on a PGCD(100,1)=1)
Donc a est premier avec 100.

[Ben314]

Salut,
Pour la question 2.1), ton raisonnement marche, mais il est bien compliqué, en particulier, il demande de dresser la liste des diviseurs impairs de 100 ce qui n'est pas franchement indispensable.
Perso, j'aurais plutôt écrit que, comme , pour qu'un entier soit premier avec 100, il faut et il suffit qu'il ne soit divisible ni par 2, ni par 5.

Pour la 2.3), faire la division euclidienne de par 100, ça consiste à écrire soit encore avec ( = quotient de la division ; = reste de la division)
Comme est multiple de 40, on a donc est un multiple de 20 donc il vaut 0 ou 20 ou 40 ou 60 ou 80.
Et on ne peut rien dire de plus car, vu que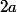 et 5 sont premiers entre eux peut prendre n'importe quelle valeur entière.