Bonsoir.
Pour la deuxième question :
L'un des nombres

et
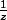
doit être de module (et donc aussi de module au carré) inférieur ou égal à 1. S'ils appartiennent tous deux à

, leur module au carré est un entier (question 1) et on en déduit qu'ils sont tous deux de module 1.
Reste à résoudre l'équation

. Pour

, on a les solutions évidents
)
et
)
qui correspondent aux nombres

et -

. De même, pour
, on a les solutions
)
et
)
qui correspondent aux nombres 1 et -1.
Pour

et

non nuls,

et

ne peuvent être de signes contraires, car le membre de gauche est alors supérieur à 3.
Mais on peut réécrire cette équation comme
^2=1-ab)
. Le membre de gauche étant positif, le membre de droite doit l'être aussi.

et

ne peuvent donc être de même signe que si leurs valeurs absolues sont inférieures à 1.
On obtient ainsi les deux dernières solutions :
)
qui correspond à

(ou -

) et
)
qui correspond à -

(soit

).
Pour conclure, on vérifie que ces six nombres
)
ont bien leur inverse dans

.
de
,
est un entier.
non nuls de
qui sont tels que
soit également élément de
?
