Exercice d'arithmétique (nombres de Fermat)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 23 Déc 2008, 19:40
par Skrilax » 23 Déc 2008, 19:40
Bonsoir,
Il y a un exercice qui me pose problème dans mon livre de spé, j'aimerais avoir quelques pistes :
x un entier strict supérieur à 1. m un naturel non nul.
Exprimer
 = 1 - x + x^2 - x^3 + ... - x^{2m-1} + x^{2m})
en fonction de x . En déduire que x+1 |

Merci.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 23 Déc 2008, 19:43
par lapras » 23 Déc 2008, 19:43
Salut, tu peux dire que -1=(-1)^(2k+1)
1=(-1)^(2k)
et utiliser la somme de suite géométrique.
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 23 Déc 2008, 19:54
par Skrilax » 23 Déc 2008, 19:54
Merci beaucoup ! on a pris un =
^{n})
et c'est bon.
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 23 Déc 2008, 20:19
par guigui51250 » 23 Déc 2008, 20:19
euh j'ai pas compris l'histoire du -1, tu pourrais m'expliquer lapras stp
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 23 Déc 2008, 21:01
par Skrilax » 23 Déc 2008, 21:01
Autre problème un peu plus loin :
m un naturel non nul, montrer que si 2^m +1 est premier alors m est de la forme 2^n avec n naturel.
Des idées ?
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 23 Déc 2008, 21:33
par Huppasacee » 23 Déc 2008, 21:33
guigui51250 a écrit:euh j'ai pas compris l'histoire du -1, tu pourrais m'expliquer lapras stp
Bonsoir
on connait la factorisation de
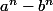
si n est impair
on peut dire que
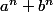
=
)
et c'est là qu'interviennent les
^n)
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 23 Déc 2008, 21:37
par Skrilax » 23 Déc 2008, 21:37
On a trouvé 2-3 trucs depuis tout à l'heure (autres questions de l'exercice) :
-q naturel strictement supérieur à 1, impair
q' naturel non-nul
2^(qq') + 1 n'est jamais premier.
- x un entier strict supérieur à 1. m un naturel non nul.
x + 1 divise x^(2m) - 1 et divise x^(2m+1) +1
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 23 Déc 2008, 21:54
par Huppasacee » 23 Déc 2008, 21:54
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 23 Déc 2008, 22:02
par Skrilax » 23 Déc 2008, 22:02
Je ne comprends pas ta réponse, ni à quelle question elle répond...
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 23 Déc 2008, 22:06
par Zweig » 23 Déc 2008, 22:06

un naturel non nul, montrer que si

est premier alors

est de la forme

avec

naturel.
L'entier

peut s'écrire sous la forme
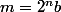
, avec

un entier naturel
impair (c'est une conséquence de la décomposition en facteurs premiers d'un entier naturel). On suppose que

est premier.
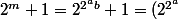^b + 1)
Or
^b + 1)
, ce qui contredit le fait que

est premier. D'où
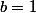
.
Rappel :
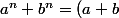(a^{n-1} + a^{n-2}b + \cdots + ab^{n-2} + b^{n-1}))
avec

impair. Donc

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
un naturel non nul, montrer que si
est premier alors
est de la forme
avec
naturel.