EDm de math sur les produit scalaire

[luciano129]

Bonjour pouvait vous m'aidez a fair mon dm de math parce que je suis totalement perdu merçi.
A(2;-1) B(3;2) C(-2;-2)
1)Déterminé une équation issue de la hauteur A et une equation de la hauteur issue de B en deduire les coordonne de l'horthocentre du triangle ABC.
2)Déterminé une équation de la mediatrice de [BC] et une équation de la médiatrice de [AC] en deduire les coordone du cercle circonscit O au triangle ABC
3)Détermine une éaquation de la droite (OH)
4)Détermine les coordonne du centre de graviré G du triangle ABC
4)Vérifier que G appartient a la droite (OH)
svp et merçi.

[fatal_error]

salut,

tu es aussi perdu niveau orthographe apparemment?

[luciano129]

wé osi mé tu peut m'aide

[fatal_error]

non. Je t'invite d'abord à lire le post-it de la section lycée, et par la même occasion à revoir l'orthographe de tes deux messages.

PS : Nous ne sommes pas sur msn, ici.

[luciano129]

SVP aide moi

[totogaga]

il a raison, surveille ton orthographe ;)

bon sinon si ton devoir appelle a l'utilisation du produit scalaire faut s'en servir essaye de determiner un produit scalaire particulier par exemple pour un point M(x,y) appartenant à la hauteur issue de A (pense a l'othogonalité)

pour la médiatrice c'est un peu pareil sauf qu'il faut trouver le milieu des cotés et former un produit scalaire particulier pour un point M appartenant a la médiatrice

en fait la technique consiste à traduire des ensembles géométriques sous forme de produits scalaires ou d'équations...

[luciano129]

Our la 1) j'ai trouvé deux équations d:-5x-4y+6=0 et d':-4x+y+14=0
mais je n'arrive pas ensuite a déterminer les coordonnées de l'orthocentre

[Ericovitchi]

tu ne sais pas résoudre ton système de 2 équations à 2 inconnues ?

[luciano129]

Non je ne sait pas le faire

[Ericovitchi]

dans la première équation tu exprimes par exemple y en fonction de x et tu remplaces dans la seconde. Tu te retrouves avec une équation où il n'y a plus que des x donc tu peux trouver x.

[luciano129]

Merçi c'est bon j'ai reussi mais je bloque ensuite pour la méditrice

[Ericovitchi]

Pour les médiatrices tu as 2 solutions : ou bien tu écris MB=MC, tu élèves au carré , les x^2+y^2 s'en vont des deux cotés et il te reste l'équation de la droite.
Ou tu fais comme quelqu'un l'a dit plus haut, tu prends le milieu I des segments, tu as un vecteur normal à BC (car si l'équation s'écrit ax+by+c=0, (a,b) est un vecteur normal ) et tu écris des équations paramétriques

[luciano129]

J'ai pas trés bien comprit

[Ericovitchi]

tu connais les coordonnées de B et C, tu cherches les points M de coordonnées (x,y) sur cette médiatrice. tu sais exprimer les coordonnées des vecteurs BM et CM et leur module (c.a.d les distances BM et CM) (un vecteur de coordonnées u,v a pour module )
tu écris donc pour qu'il n'y ait plus de racine. Tu développes, tu simplifies (car les 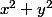vont s'en aller des deux cotés) et tu trouves ton équation de droite.

[luciano129]

Non je vois vraiment pas du tout
mais en tout cas merçi de m'aide

[Ericovitchi]

tu as une façon peut être plus simple.
Calcules les coordonnées du milieu I de BC et écris que le produit scalaire IM.BC= 0 ça te donnera l'équation de la droite.

[luciano129]

je ne voit pas de quelle M vous parlez.

[Ericovitchi]

M le point courant de la médiatrice, celui qui a pour coordonnée (x,y) et qui parcourt la droite dont tu veux chercher l'équation
C'est quoi une médiatrice ? c'est le lieu des points M tel que IM est perpendiculaire à BC ? donc tel que

C'est sûr que si tu ne maîtrise ni le produit scalaire, ni la distance entre deux points, ni ce qu'est une médiatrice, etc... tu vas avoir du mal à finir l'exercice.