Petit question de suite

par **Fess2bab** » 24 Mai 2009, 10:15

Bonjour à tous,

Je dois déterminer que la suite Un est croissante donc je me décide naturellement à faire Un+1 - Un =, mais cette fois ci la fontion n'est pas aussi simple que d'habitude et je suis donc coincé. Pourriez vous me donner un petit coup de pouce ?

La fonction tirée d'une intégrale est : 1/(1+t+t^n)

et je suis actuellement là : 1/(1+t+t^n+1) - 1/(1+t+t^n) =

A savoir que j'ai deja Uo et U1 et que la question précédente m'a permis de déterminer que Un>0.

Merci :)

par **sky-mars** » 24 Mai 2009, 10:31

Salut ^^ :)

Un+1 - Un de maniere direct n'est pas top
faudrait genre tu fasses une démo du type
Vx [ a , b ] , f ( x) < g ( x )

=> int ( f ( x ) , x= a..b ) < int ( g ( x ) , x=a..b )
=> Un < Un+1
=> Un+1 - Un > 0 AQT
une démo dans ce genre la !
maintenant a toi d'adapter

par **Fess2bab** » 24 Mai 2009, 10:34

sky-mars a écrit:Salut ^^

Un+1 - Un de maniere direct n'est pas top
faudrait genre tu fasses une démo du type
Vx [ a , b ] , f ( x) int ( f ( x ) , x= a..b ) Un Un+1 - Un > 0 AQT
une démo dans ce genre la !
maintenant a toi d'adapter

Tout d'abord merci de te pencher sur mon problème

J'aurai juste une question, qu'entends tu pars AQT ?

par **sky-mars** » 24 Mai 2009, 10:36

aaaaaaaaaaah lol fait pas attention à l' AQT , sa signifie âne qui trotte mdr :D
c'est comme si tu disais CQFD (ce qu'il fallait demontrer )

par **Ericovitchi** » 24 Mai 2009, 10:36

penses aussi à faire Un+1/Un
dans le cas présent il est assez facile de trouver sa limite, son signe, si c'est plus grand que 1 ou pas, ...

par **sky-mars** » 24 Mai 2009, 10:38

oui mais la , c'est des suites définie par des intégrales non ? c'est pas top le rapport d'intégrale il me semble .
Sauf erreur de ma part en comprenant mal l'énoncé

par **Ericovitchi** » 24 Mai 2009, 10:41

ha je n'ai pas compris ? Un= 1/(1+t+t^n) ou bien il y a une intégrale sur t ? de quoi à quoi l'intégrale ?

par **sky-mars** » 24 Mai 2009, 10:44

je suis okey avec erico si Un c'est fonction , le rapport est plus simple a étudier puis de comparer si c'est > ou < à 1
Par contre si Un est définie par une intégrale ,ce que je t'ai proposé est OK

par **Fess2bab** » 24 Mai 2009, 10:48

je vous donne l'énoncé tel quel sa vous permettra d'etre tous d'accord.. lol

Pour tout n de IN, on pose Un = S:0à1 1/(1+t+t^n) dt et on a, en particulier, Uo= S:0à1 1/(2+t) dt

(S:0à1 pour dire Intégrale de 0 à 1)

par **Fess2bab** » 24 Mai 2009, 10:55

1) Pour tout n de IN, justifier l'existence de Un
J'ai demontré que Un est continue sur son Df en tant que fonction rationnelle donc elle est définie sur son intervalle.
2) Calculer Uo et U1
Uo j'ai trouvée Ln 3/2 et U1 j'ai trouvé (1/2) Ln 3 (Linearité)
3) a. Montrer que Un > 0
- Les bornes sont croissantes [0;1]
- 1/1+t+t^n > 0 car 1>0 et Le polynôme 1+t+t^n >0
Donc on peut conclure que Un > 0
b. c'est la question que je vous est posée

par **sky-mars** » 24 Mai 2009, 10:57

OKEY
V t [0, 1] , 1/(1+t+t^n) < 1/(1+t+t^n+1) (*)

=> int ( 1/(1+t+t^n) dt ,0à1) < int (1/(1+t+t^n+1) dt, de0 à 1 )

Démontre (*) dans un premier temps
il sera plus simple d'étudier l'inverse ...
i.e 1 + t + t^n
Puis ensuite tu intégres l'inégalité et aprés c'est fini

par **sky-mars** » 24 Mai 2009, 11:01

voui c'est ce que j'avais bien pensé pour l'étude de l'inverse ^^ :D
c'est fou du pathééééé tout ca mdr

par **Fess2bab** » 24 Mai 2009, 11:10

Comment voulez vous que je démontre Un+1 ?
La methode que vous me proposé a un nom ? si des fois je peux le glisser..

par **sky-mars** » 24 Mai 2009, 11:19

C'est la méthode " je connais mon cours " mdr :D

beh
Vt [ 0, 1 ], VnN (1+t+t^n+1) < (1+t+t^n)
=>Vt [ 0, 1 ] VnN , 1/(1+t+t^n+1) > 1/ (1+t+t^n)
( et la tu montres que tu connais ton cours sur l'intégration )
=>VnN , intégrale ( (1+t+t^n+1) ) (t=0..1) > intégrale( (1+t+t^n) ) (t=0..1)
=> VnN Un+1 > Un
=> VnN Un+1 - Un > 0
=> (Un) est croissante

par **Fess2bab** » 24 Mai 2009, 11:26

sky-mars a écrit:C'est la méthode " je connais mon cours " mdr

beh
Vt [ 0, 1 ], VnN (1+t+t^n+1) Vt [ 0, 1 ] VnN , 1/(1+t+t^n+1) > 1/ (1+t+t^n)
( et la tu montres que tu connais ton cours sur l'intégration )
=>VnN , intégrale ( (1+t+t^n+1) ) (t=0..1) > intégrale( (1+t+t^n) ) (t=0..1)
=> VnN Un+1 > Un
=> VnN Un+1 - Un > 0
=> (Un) est croissante

Et la démonstration permet de dire que Un est croissante ou je dois le déterminer par le calcul ?

par **sky-mars** » 24 Mai 2009, 11:29

on ne détermine rien par le calcul .
La démonstration est juste au dessus et sa se tient en quelques lignes.

Ta question était montrer que Un croissante donc tout ce que j'ai fait c'était que pour tout entier naturel n , on a : Un+1 > Un
j'ai démontré cette inégalité , et retient le schéma de démonstration car c'est comme ca qu'on fait quand on a des suites définie par des intégrales

par **Fess2bab** » 24 Mai 2009, 11:35

D'accord, je n'es pas beaucoup travaillé ce raisonnement encore c'est pour ça.
La dernière question de l'exercice me demande de démontrer que VnN, Un <= ln2.
Comment procéder ?

par **busard_des_roseaux** » 24 Mai 2009, 11:38

Bj,

à t fixé,dans [0;1] , la suite

décroit.

ex:

en passant à l'inverse

à t fixé,dans [0;1] , la suite

est croissante.

donc les deux fonctions

et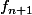

définies par:

vérifient

en les intégrant de [0;1], on obtient une suite d'intégrales (strictement) croissante.

Ln(2) est l'intégrale de la fonction

c'est à dire .......?

par **sky-mars** » 24 Mai 2009, 11:42

tu as
1+t < 1+t+t^n Vt[0,1] VnN
donc

1/(1+t) > 1/ (1+t+t^n )

ensuite tu intégres ... comme tout a l'heure

et int ( dt/(1+t ) , t=0..1 ) = ln2
d'ou le résultat..

par **Fess2bab** » 24 Mai 2009, 11:44

??? ça valide ce qui avait été dit ?

Petit question de suite

Petit question de suite

Qui est en ligne