Un petit mot sur la suite de Fibonacci

[Aspx]

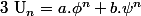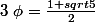Il est facile de démontrer que toute suite qui s'écrit : (où et 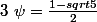et a et b des constantes) est une suite vérifiant 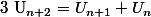. Mais qu'en est-il de la réciproque ? Quelqu'un aurait une idée ? Ca risque d'utiliser des notions que j'ai pas encore globalement étudié mais ma curiosité est trop grande v_v.
Merci :we:

[sue]

salut


donc l'équation caractéristique est : qui admet 2 solutions : et
donc l existe t.q :

[Aspx]

En gros j'aimerais savoir oui comment Binet trouva . Si j'ai le résultat de cette réciproque on a plus qu'à trouver a et b en fonction de F0 et F1

[Aspx]

Oui ok pour l'équation caractéristique, ça se traite comme les équations différentielles m'a dit mon prof mais... la démonstration svp :we:

[sue]

et sont solutions de donc les suite et vérfient la relation
on a alors :

[Aspx]

et sont solutions de donc les suite et vérfient la relation
on a alors :

Tu as "montré" là juste que toute suite qui s'écrit vérifie la relation. Et non que toute suite qui vérifie la relation s'écrit

[sue]

donc l'équation caractéristique est : qui admet 2 solutions : et
donc l existe t.q :

ça ne suffit pas ?

en général : (suite reccurente linéaire )
l'équation caractéristique :
- si (l'équation admet 2 solutions et ) alors t.q :

[Aspx]

Surement mais j'aurais aimé la démonstration, le "alors il existe"

[sue]

et sont solutions de donc les suite et vérfient la relation

alors aprés tu sais que si et vérifient (E') : alors toute combinaison linéaire de et vérifie E' ?(c facile à démontrer)

alors dans notre cas : et vérifient (E) donc la vérifie également .

si est une suite vérifiant (E) alors : t.q :

oK ?

[Aspx]

Non c'est faux, rien ne te dis que toute suite récurrente linéaire de cette forme s'écrit comme ça !
C'est comme quand tu fais des lieux de points. Si un point vérifiant la condition se trouve sur un cercle donné ça veut pas dire que le lieu des points est tout le cercle, il faut prendre un point quelconque du cercle et montrer qu'il vérifie la condition.
Si on note E l'ensemble des suites réelles telles que 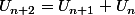et F l'ensemble des suites réelles telles que 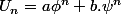, on vient de montrer que F est inclus dans E, et non que E est inclu dans F !