Bonjour,
je ne sais comment m'y prendre avec l'exercice suivant :
D'abord il faut déterminer le rang de la matrice réelle
A=[1,2
2,4]
qui est 1 ...
Ensuite, deuxième question, soit n un entier naturel non nul. Résoudre l'équation
X^n = A où l'inconnue X est une matrice réelle carrée d'ordre 2.
Quel est le rapport avec la question précédente ? je ne vois pas le lien :s
merci d'avance pour tout conseils !
[sup] équation matricielle
6 messages
- Page 1 sur 1
merci ! 
je crois avoir compris, et donc on obtient pour n entier non nul :
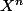 = [
= [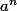 ,
, 
0, 0].
Avec a = 1 et b = 2.
car A étant de rg 1, on ne peut avoir X de rg 2, ni X^n, et a fortiori X^(-n).
si rg X = 0, alors X est la matrice nulle, et donc ne peut être égale à A, lorsque élevée à n'importe quelle puissance.
je crois avoir compris, et donc on obtient pour n entier non nul :
0, 0].
Avec a = 1 et b = 2.
car A étant de rg 1, on ne peut avoir X de rg 2, ni X^n, et a fortiori X^(-n).
si rg X = 0, alors X est la matrice nulle, et donc ne peut être égale à A, lorsque élevée à n'importe quelle puissance.
Es-tu en train de croire que la solution de X^n=A est la même quel que soit A?
A chaque n son équation et donc son ensemble de solution.
NB tu peux poser a,b;ka,kb mais il faut expliquer pourquoi. En effet, deux vecteurs sont liés si et seulement s'il existe lambda et mu (non tous les deux nuls) tels que:
On ne pourra écrire u=kv que si v est non nul.
A chaque n son équation et donc son ensemble de solution.
NB tu peux poser a,b;ka,kb mais il faut expliquer pourquoi. En effet, deux vecteurs sont liés si et seulement s'il existe lambda et mu (non tous les deux nuls) tels que:
On ne pourra écrire u=kv que si v est non nul.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
