Comparaison de nombre A et B
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 22:50
par cvnc » 23 Avr 2009, 22:50
Bonsoir à toi aussi, bienvenue sur le forum ...
Je dois comparer A et B dont A= a+b divisé par 2 et B= 2ab divisé par a+b
J'ai tenter de faire la difference de ses deux nombres pour etudier le signe sans la moindre idée du pourquoi du comment...
J'ai trouver:
B-A= 6ab-a²+b² divisé par 2(a+b)
merci d'avance à ceux qui m'aideront
EDIT : la politesse est une valeur qui se perd ...
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:14
par cvnc » 23 Avr 2009, 23:14
ho oui pardon tellement preocupée par mon exercice j'en ai oublié la politesse.
alors heu... Bonsoir... (vaut mieu tard que jamais!)
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:15
par uztop » 23 Avr 2009, 23:15
Salut,
est ce que tu es sûr de ton énoncé ?
Ca ne serait pas A=a+b et
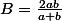
que tu dois comparer plutôt ?
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:17
par cvnc » 23 Avr 2009, 23:17
non non mon enoncé et bien celui que j'ai donner ci dessus
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:19
par uztop » 23 Avr 2009, 23:19
ok, et qu'est ce que tu sais sur a et b ? Ils sont tous les deux
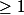
?
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:20
par cvnc » 23 Avr 2009, 23:20
ils sont strictement possitifs!
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:25
par uztop » 23 Avr 2009, 23:25
et ce sont des entiers ?
A et B sont donc tous les deux positifs, tu peux donc calculer B/A (A ne peut pas être nul). Quelle est la condition pour que B>A ?
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:26
par cvnc » 23 Avr 2009, 23:26
aucune information la dessus se sont 2 réel strictement positif et il faut les comparer c'est tout ce que je sais :s
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:28
par uztop » 23 Avr 2009, 23:28
oui, et donc B/A, ça donne quoi ?
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:30
par cvnc » 23 Avr 2009, 23:30
mais pourquoi tu veux diviser?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:30
par uztop » 23 Avr 2009, 23:30
eh bien si B>A, B/A >1
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:32
par cvnc » 23 Avr 2009, 23:32
et comment je peux savoir si c'est superieur a 1 puisque je connais ni a ni b
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:36
par uztop » 23 Avr 2009, 23:36
justement, il faut des hypothèses supplémentaires sur a et b (genre supérieurs à 1), c'est pour ça que je te demandais si ils étaient supérieurs à 1.
Si tu ne sais rien de plus, tu ne peux pas conclure.
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:40
par cvnc » 23 Avr 2009, 23:40
le titre de la partie c'est etudier le signe de la difference... D'ou mon calcul de depart mais je ne sais pas comment definir le signe de mon resultat ni comment comclure a ma comparaison...
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:45
par uztop » 23 Avr 2009, 23:45
ok, si le problème te dit explicitement d'étudier le signe de la différence, on peut faire comme ça, mais sans plus d'hypothèses sur a et b on ne pourra pas conclure non plus.
Mais je ne comprends pas comment tu arrives à
})
; il y a certainement une erreur de calcul quelque part.
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:50
par cvnc » 23 Avr 2009, 23:50
deja je commence par mettre les 2 nombres au meme denominateur pour pouvoir les soustrairent ensuite.
j'obtiens
B-A= 2abx2/2x(a+b) - (a+b)x(a+b)/2(a+b)
en developpant je remarque une identité remarquable dans A.
je developpe je rassemble les ab et j'obtien ce resultat! apres y'a peut etre une erreur de calcul mais je vois pas...
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Avr 2009, 23:55
par uztop » 23 Avr 2009, 23:55
oui, je suis d'accord sur la méthode.
Je pense que tu as fait une erreur sur les parenthèses.
Pour le numérateur, on a 4ab-(a²+2ab+b²) = 2ab-a²-b² ; est ce que tu es d'accord ?
-
cvnc
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Avr 2009, 22:45
-
 par cvnc » 23 Avr 2009, 23:56
par cvnc » 23 Avr 2009, 23:56
ho oui! je l'avais pas vu celle la merci ^^
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 24 Avr 2009, 00:00
par uztop » 24 Avr 2009, 00:00
bon, maintenant tu peux reconnaitre une identité remarquable dans 2ab-a²-b² (oui en fait on peut conclure sur le signe de B-A)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
