Exemples de sous variétés !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 17:22
par barbu23 » 28 Jan 2009, 17:22
Bonjour :
Pourquoi les deux ensembles suivantes ne representent pas des sous variétés differentiables alors que le troisième est une sous variété :
 \hspace{4cm} \{ \hspace{2cm} (x,y,z) \in \mathbb{R}^3 \hspace{2cm} | \hspace{2cm} x^2 + y^2 - z^2=0 \hspace{2cm} \} $)
 \hspace{4cm} \{ \hspace{2cm} (x,y) \in \mathbb{R}^2 \hspace{2cm} | \hspace{2cm} x^2 - y^2 =0 \hspace{2cm} \} $)
 \hspace{2cm} \{ \hspace{2cm} (t^2,t^3) \hspace{2cm} | \hspace{2cm} t \in \mathbb{R} \hspace{2cm} \} $)
Par contre, dans le cours, on dit que
 $)
est une sous variétés pour :

un difféomorphisme !
Merci d'avance de votre aide !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 17:25
par barbu23 » 28 Jan 2009, 17:25
Est ce que parceque les

représentant chacun des deux premiers ensembles ne sont pas des submersions ? C'est peût etre à cause de celà ! n'est ce pas ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 17:32
par barbu23 » 28 Jan 2009, 17:32
Pourquoi le troisième ensemble est une sous variété ?
Merci d'avance !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 28 Jan 2009, 17:32
par Nightmare » 28 Jan 2009, 17:32
Salut !
As-tu essayé avec des arguments de connexité?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 28 Jan 2009, 17:51
par ffpower » 28 Jan 2009, 17:51
As tu essayé de les dessiner?Bon le 1er,c est pas pratique car dans l espace,mais dessine le 2eme et tu devinera pourquoi c est pas une variété(différentiable..c est une variété topologique par contre)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 18:15
par barbu23 » 28 Jan 2009, 18:15
Re "Nightmare" :
Je ne vois pas encore le rapport avec la connexité ! Mon cours ne comporte aucune notion de connéxité dans ce chapitre sur le concept des sous variétés ! Je pense qu'il ne faut utiliser que des arguments juste avec l'emploi des définitions et ce qu'il y'a dans n'importe quel cours pour debutants ! mais, je ne vois pas encore comment !
Dans un autre cours :
 \hspace{2cm} | \hspace{2cm} x^2 + y^2 + z^2 - 1 = 0 \hspace{2cm} \} $)
est une sous variété.
Par contre, l'ensemble suivant qui ressemble un peu à celui de çi-dessus n'est pas une sous variété :
 \hspace{2cm} | \hspace{2cm} x^2 + y^2 - z^2 = 0 \hspace{2cm} \} $)



Merci d'avance de votre aide !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 18:18
par barbu23 » 28 Jan 2009, 18:18
ffpower a écrit:As tu essayé de les dessiner?Bon le 1er,c est pas pratique car dans l espace,mais dessine le 2eme et tu devinera pourquoi c est pas une variété(différentiable..c est une variété topologique par contre)
D'accord, je vais essayer, merci !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 20:03
par barbu23 » 28 Jan 2009, 20:03
Re-Bonsoir :
ffpower a écrit:As tu essayé de les dessiner?Bon le 1er,c est pas pratique car dans l espace,mais dessine le 2eme et tu devinera pourquoi c est pas une variété(différentiable..c est une variété topologique par contre)
J'ai tracé le graphe du deuxième ensemble et je trouve qu'il est sos la forme d'un croix ! pourquoi celà signifie que l'ensemble sous entendu n'est pas une sous variété ? Qu'est ce qu'il a de particulier par rapport aux autres variétés différentiables ?
Merci infiniment !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 20:44
par barbu23 » 28 Jan 2009, 20:44
Svp aidez moi ! merci d'avance !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Jan 2009, 23:35
par barbu23 » 28 Jan 2009, 23:35
Help please ! :hum: :cry: :cry: :cry:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Jan 2009, 23:57
par Doraki » 28 Jan 2009, 23:57
Pour la deuxième, est-ce que tu trouves un voisinage de (0,0) tel que la variété y est difféomorphe à un ouvert de R ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2009, 00:10
par barbu23 » 29 Jan 2009, 00:10
Doraki a écrit:Pour la deuxième, est-ce que tu trouves un voisinage de (0,0) tel que la variété y est difféomorphe à un ouvert de R ?
Au voisinage de
 $)
: la variété n'est pas difféomorphe ( d'après le graphe ) Ils possède deux dérivée je pense ! Mais je ne sais pas comment la démontrer ! :doh:

Aidez moi svp et
Merci infiniment ! :happy2:
-
Prison Break
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Nov 2006, 14:42
-
 par Prison Break » 29 Jan 2009, 15:14
par Prison Break » 29 Jan 2009, 15:14
barbu23 a écrit:Au voisinage de
 $)
: la variété n'est pas difféomorphe ( d'après le graphe ) Ils possède deux dérivée je pense ! Mais je ne sais pas comment la démontrer ! :doh:

Aidez moi svp et
Merci infiniment ! :happy2:
La définition d'une sous-variété de 
(d'aprés mon cours de géo. diff de L3):
soit

une partie de

.
On dit que

est une sous-variété de classe
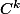
et de dimension

si et selment si pour tout point

, il existe un ouvert

de

et un
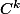
-difféomorphisme
)
, tel que
=f(U) cap \R^m)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2009, 16:37
par barbu23 » 29 Jan 2009, 16:37
Prison Break a écrit:La définition d'une sous-variété de 
(d'aprés mon cours de géo. diff de L3):
soit

une partie de

.
On dit que

est une sous-variété de classe
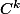
et de dimension

si et selment si pour tout point

, il existe un ouvert

de

et un
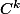
-difféomorphisme
)
, tel que
=f(U) cap \R^m)
Oui, c'est ce que j'essaye d'appliquer mais en vain !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
: la variété n'est pas difféomorphe ( d'après le graphe ) Ils possède deux dérivée je pense ! Mais je ne sais pas comment la démontrer ! :doh:

(d'aprés mon cours de géo. diff de L3):
une partie de
.
est une sous-variété de classe
et de dimension
si et selment si pour tout point
, il existe un ouvert
de
et un
-difféomorphisme
, tel que