Sous-variétés et géométrie

[Aispor]

Bonsoir,
je dois faire un exercice que je ne comprend pas vraiment
Enfin je comprend la question mais je ne vois pas du toute comment m'y prendre :



Gloire à celui qui voudra bien m'aider !

[mathelot]

Bonsoir
Pour la 1) regarder ce qui se passe dans une carte.
Pour la 2) soit la courbe plane dans un repère d'équation
x=(1-t^2) /(1+t^2),y=2t/(1+t^2)

[Aispor]

Salut, merci d'avoir répondu !

Pour la première question donc j'ai pris cette définition pour les sous-variétés :



Soit M une sous-variété connexe de dimension 1 dans
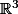
un point de M
Il existe donc un voisinage de noté et un voisinage de noté
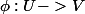
ainsi qu'un difféo tel que

où est l'ensemble

j'aimerais pouvoir donc dire que, étant un difféo de
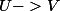
On a
Reste à justifier pourquoi est une courbe régulière.
Le fait que la dérivée est non-nulle provient du fait que c'est un diffeo.
Le fait qu'on puisse la paramétrée provient du fait que c'est définie sur un voisinage ouvert de (car les cordonnée d'ordonnée et la côte sont nulles)
Mais je n'utilise pas la connexité de M.

Pour le contre exemple je ne vois pas pourquoi ça n'est pas une sous-variété de dimension 1 car une fois tracée la courbe donnée est un cercle, et pourtant on a vu que c'est bien une sous-variété de dimension 1

Merci !

[Aispor]

Peut-être devrais-je utiliser la caractérisation des sous-variétés avec les paramétrages. Mais je ne vois pas où intervient la connexité encore.

[aviateur]

Bonjour
Sauf erreur de ma part le fait que la variété soit connexe ne joue qu'un rôle secondaire.
Une courbe régulière peut avoir plusieurs composantes connexes (à vérifier).
Maintenant je en comprend pas l'exempel de @mathelot.
Car la courbe est le cercle C(O,1) privé du point (-1,0). Le paramétrage définit un difféormorphisme entre la courbe et

[mathelot]

bon, je me suis planté, le point asymptote ne fait pas partie de la courbe.la question 2 reste donc en suspend

Il faudrait trouver le support d'une courbe régulière , et un point de cette courbe, dont tout voisinage ne peut être localement difféomorphe à un intervalle: on peut essayer la lemniscate de Bernoulli (à cause du point double)

https://fr.wikipedia.org/wiki/Lemniscate_de_Bernoulli

[aviateur]

Oui exactement la lemniscate n'est pas une variété à cause du point double en (x,y)=(0,0)

[Aispor]

Merci
De plus pour les questions précédentes, je les ai fait de la même manière.
Un point me chagrine cependant : La définition de surface régulière.
Est-ce simplement une sous-variété de dimension 2 ?

[aviateur]

Pour moi une surface régulière est un sous ensemble de qui peut être définie implicitement par une équation de la forme f(x,y,z)=0
ou alors paramétriquement par une fonction g de classe
I,J étend des intervalles.
La surface est régulière en si