Question de Cours Sous variétés

[Kimou]

Bonjour,
j'essaye de bien comprendre les sous variétés et voici ma question:
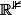
Soit une fonction, si je montre que la jacobienne est toujours de rang 2 pour tout x,y,z c'est ok, il s'agit d'une sous variété de , de dimension 1.

Mais disons qu'on trouve que le rang est pour tout x,y,z toujours égal à 1 alors que peut on dire? Est-ce une sous variété? De quelle dimension?
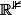
Par ailleurs si on trouve 2 points tels que la jacobienne en ces points soit de rang différents pour chacun d'eux, si les 2 points appartiennent de plus à f alors f n'est pas une sous variété de , mais si l'un des 2 points en fait n'appartient pas à f alors il peut exister une sous variété non?
Merci

[Kimou]

Personne ?

[Ben314]

Salut,
Bon, pour commencer, la façon de poser le problème ne va pas du tout : dire que "des points appartiennent à f" ou que "f est une sous variété" est... sans queue ni tête : f est une application donc elle ne risque pas de "contenir" quelque chose et encore moins d'être une sous variété.

Bon, concernant ta première affirmation, c'est ce que l'on appelle "le lemme de la submersion" qui est un corollaire du théorème des fonction implicites (lui même corollaire du théorème d'inversion locale) : c'est une des pierres angulaires pour définir des sous variétés de R^n. (si tu n'as pas le théorème EXACT, regarde sur Wiki.)

Ta deuxième question (si le rang est constant égal à 1...) correspond trés précisément au "théorème du Rang" (appellé aussi Lemme de la subimmersion) : Si f est C1 d'un ouvert Omega de R^n dans R^p, et si a appartenant à Omega est tel que df soit de rang constant au voisinage de a alors, au voisinage de a, l'ensemble M=f^{-1}(f(a)) est une sous variété de R^n de dimension n-Rang(df(a)).

Concernant ta troisième question, je vois vraiment pas ce que pourrait vouloir dire "deux points appartiennent à f"...

[Kimou]

Merci pour ces réponses. Oui j'ai voulu aller vite mais c'est vrai que c'est vraiment moche je voulais dire pour ma troisième question, dis autrement:

Si tout point vérifiant l'équation donné par f, tel que, la différentielle de f en ces points soit de rang constant et si on arrive à trouver certains autres points qui changent le rang de la jacobienne mais qui ne vérifie pas l'équation donnée par f peut on dire que le sous ensemble {/ tel que les équation soient vérifiées} est une sous variété de ?

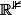
[Ben314]

J'ai pas de contre exemple en tête, mais je suis pas sûr du tout que ça marche dans ce cas :
Si tu prend un point du sous ensemble en question, tu ne sais pas si le rang est constant au voisinage du point (car il n'y a aucune raison qu'un voisinage du point soit contenu dans le sous ensemble en question) donc tu ne peut pas appliquer le lemme de la subimmersion.

Pour être sûr que le résultat soit valable, il faudrait que le rang soit constant sur un voisinage du sous ensemble en question (c'est à dire, quitte à diminuer Omega, que f soit de rang constant sur Omega et... on retombe sur le lemme de la subimmersion)
Vu que la fonction "rang" est semi continue inférieurement, il suffit par exemple de savoir que le rang de f est constant sur le sous ensemble en question et que cette constante est en fait le maximum du rang de f sur Omega.