Ensemble des complexes de module 1

[flocaz]

Bonjour à tous !

Voilà, j'ai un exo, et j'ai vraiment du mal à partir...

Soit Um et Un deux ensembles ( avec U l'ensemble des complexes de module 1)

Um est inclu dans Un <=> m | n

j'ai essayé de me servir de la définition, à savoir Un = { exp ( k2Pi / n ) ; avec k appartient à [|0;n-1|] }, mais je ne vais pas bien loin.

merci d'avance a ceux qui pourront m'éclairer ;)

[adrienhardy]

Bon déjà l'implication (<=) est évidente
(si ce n'est pas le cas, réécris la définition de m|n)

Pour l'autre sens,
si il existe par hypothèse un certain k' tel que
. Tu prends le log de tout ça (n'oublie pas qu'on travaille modulo 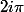) et tu conclus que m|n (là il va falloir utiliser le lemme de Gauss).

bonne journée

[flocaz]

Merci pour ta réponse ;)

Par contre, quand tu me dis de prendre de log, j'arrive ensuite à quelque chose comme :

m (k'/k) = n... mais je ne sais pas si ce (k'/k) est un entier ?

merci encore ;)

[Maxmau]

Bj

Un est le groupe des racines n-ièmes de l’unité
Un = {z complexes : z^n =1} = {Exp(2ik;)/n) : k = 0,1,2,…,(n-1)}
Dans l’hypothèse où m divise n, l’égalité z^m =1 entraîne z^n =1. Conclusion : Um contenu dans Un
Réciproquement, dans l’hypothèse où Um contenu dans Un , Exp(2i;)/m) est dans Un d’où : [Exp(2i;)/m)]^n = 1 soit encore Exp(2i;)n/m) =1 ce qui implique m divise n (n/m est un entier)


Rappel : Exp(ix) = 1 ss x est un multiple entier de 2;)

Remarque : la réciproque peut encore se traiter en disant que l’ordre de Um ( Um est un sous-groupe de Un) divise l’ordre de Un (théorème de Lagrange)

[flocaz]

merci bien, j'vais cogiter ca ;)
bonne soirée !