Démonstration avec suite et partie entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bart22
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Sep 2008, 19:22
-
 par bart22 » 29 Nov 2008, 13:48
par bart22 » 29 Nov 2008, 13:48
Bonjour,
On pose M= l(E(x) + 1).
je dois montrer que:
Un < M
sachant que:
. Un = l(xn) - nl(10)
.xn= E(10^n x)
.10xn < xn+1
.xn diverge vers +infini
.Un est croissante
Une aide serait la bienvenue. Merci d'avance.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 29 Nov 2008, 21:53
par fatal_error » 29 Nov 2008, 21:53
Bonjour,
je pense pas pouvoir resoudre, mais ca veut dire quoi l?
genre l(E(x)+1)
la vie est une fête

-
bart22
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Sep 2008, 19:22
-
 par bart22 » 30 Nov 2008, 11:41
par bart22 » 30 Nov 2008, 11:41
Peut-être qu'il manque es infos:
. l(k) est la limite commune des suites :
Un = 1/(n+1) + ... + 1/(kn)
Vn = 1/n + ... + 1/(kn-1)
. l(1)=0
. l(kk')=l(k)+l(k')
. 1/(k+1) < l(k+1) - l(k) < 1/k
. l est croissante

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Nov 2008, 12:41
par fatal_error » 30 Nov 2008, 12:41
Je pense avoir une piste:
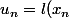-nl(10)=l(x_n)-l(10)-(n-1)l(10)\\<br />l(kk')=l(k)+l(k'))
donc
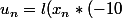) -(n-1)l(10))
...
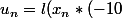^n)))
Le problème, c'est qu'on veut majorer u_n :
en utilisation le fait que l est croissante, on doit avoir
^n0, donc il suffit de faire ca sur une somme de positifs ce qui revient a : <br />[TEX]u_n l(x_n)<l(\alpha)+nl(10))
donc on fait pareil pour le membre de droite, et c'est comfortable .
<l(\alpha * 10^n))
Et pis la je pense qu'on utiliser le fait que l est croissante.
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
